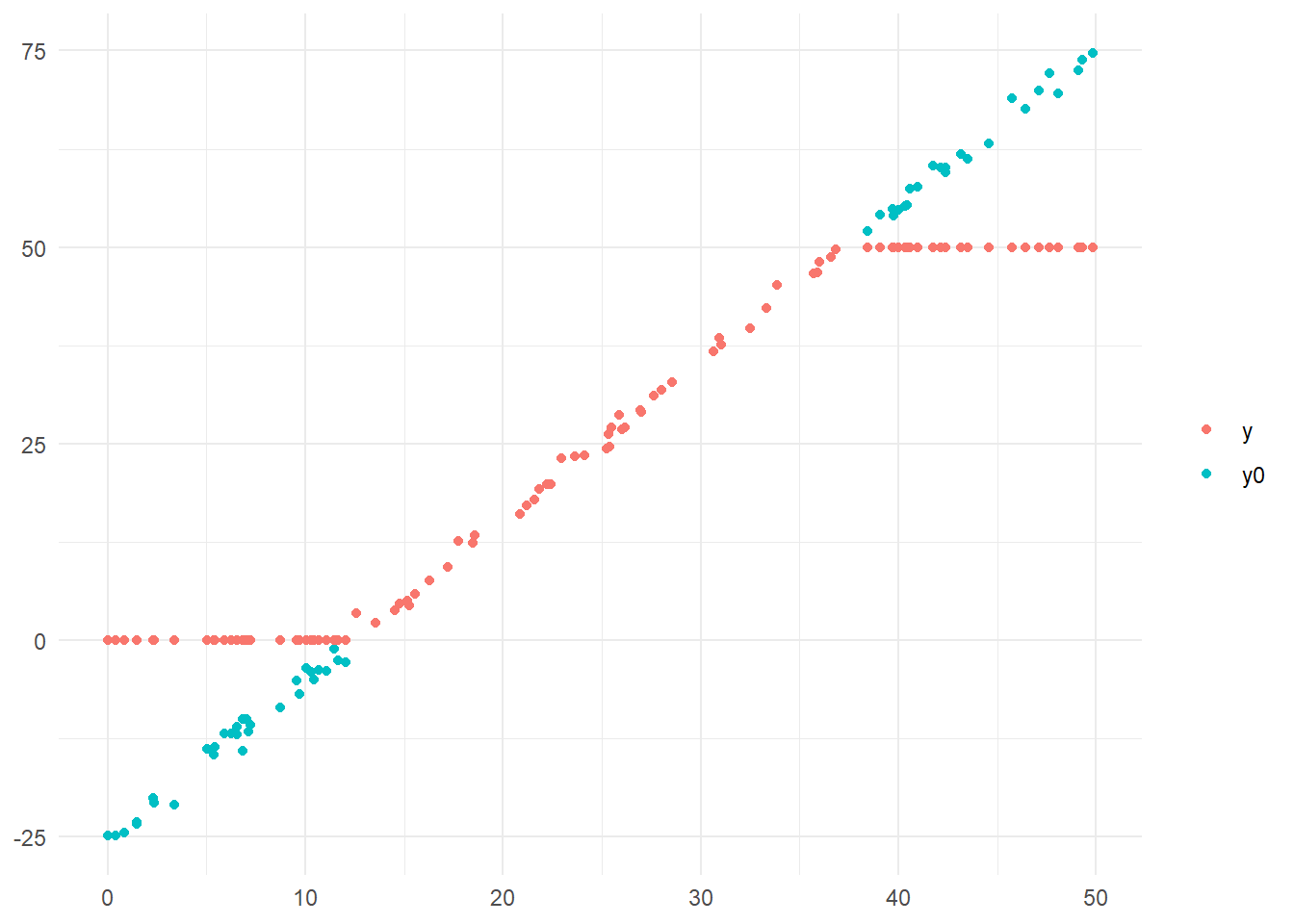
# サンプルデータの作成
library(VGAM)
library(dplyr)
library(ggplot2)
set.seed(20230426)
n <- 100
x <- runif(n = n, min = 0, max = 50)
b0 <- -25
b1 <- 2
y0 <- b0 + b1 * x + rnorm(n = n)
y <- y0 %>%
{
ifelse(. > 50, 50, ifelse(. < 0, 0, .))
}
tidydf <- data.frame(x, y0, y) %>%
{
tidyr::gather(data = ., key = "key", value = "value", colnames(.)[-1])
}
(g <- ggplot(data = tidydf, mapping = aes(x = x, y = value, col = key)) + geom_point() + theme_minimal() + theme(legend.title = element_blank(), axis.title = element_blank()))Rで回帰分析:トービット・モデル
Rでデータサイエンス
トービット・モデル
\[ \begin{eqnarray} \textrm{y}_i^{\ast}&=&\mathrm{\beta\,x}_i+\textrm{u}_i\\ \textrm{y}_i &=&\left\{ \begin{array}{ll} 0 & (\textrm{y}^{\ast}_i \leq 0)\\ \textrm{y}^{\ast}_i & (\textrm{y}^{\ast}_i >0) \end{array} \right. \end{eqnarray} \] 『通常の最小二乗法による推定量はバイアスがあることが知られており,最小二乗法は\(\,\mathrm{\beta}\,\)の推定に使うことはできず,最尤法に基づく推定量が推定に用いられる。』 - 出所: https://dl.ndl.go.jp/view/prepareDownload?itemId=info%3Andljp%2Fpid%2F11172411&contentNo=1
サンプルデータの作成
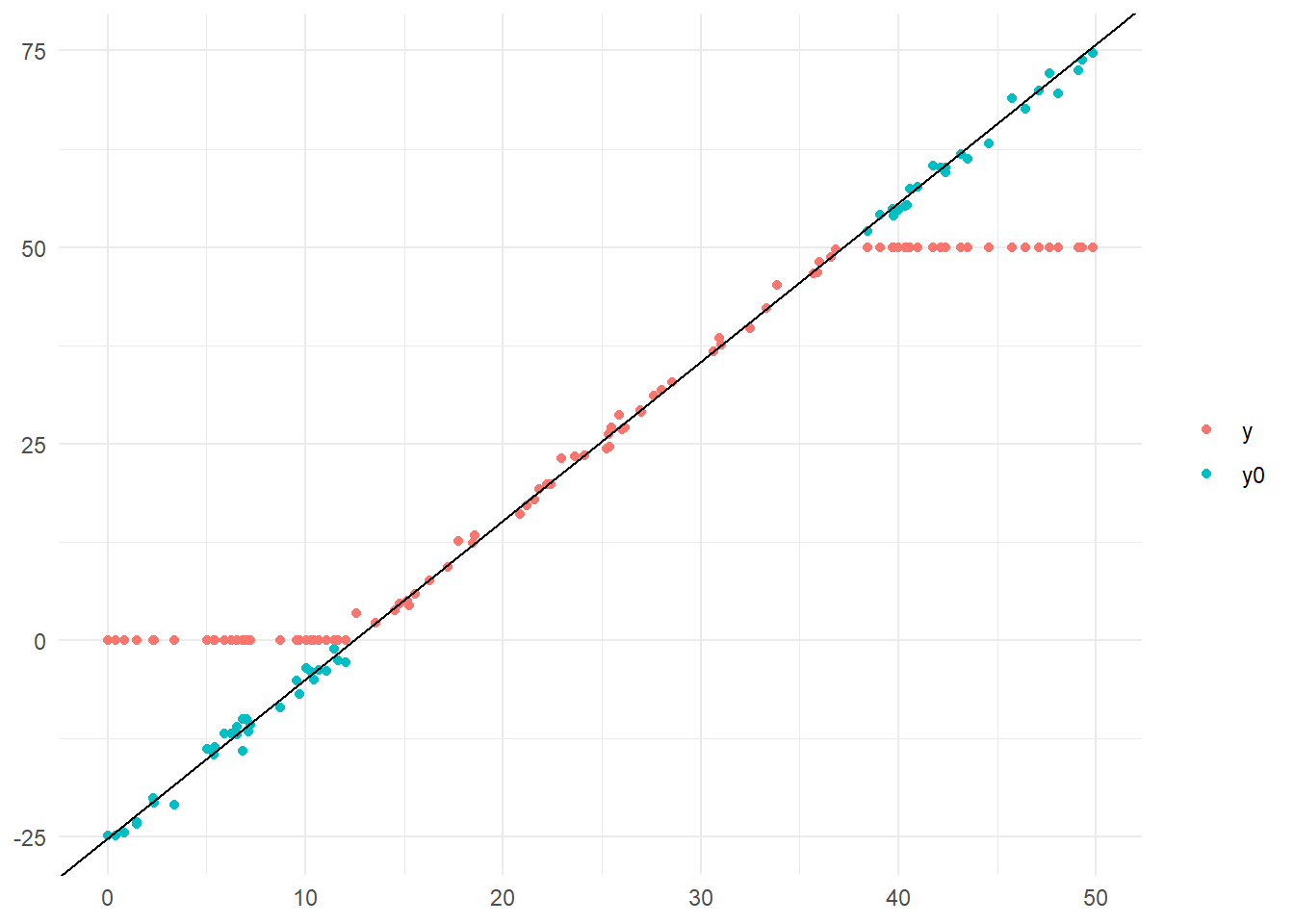
トービット・モデル
# トービット・モデル
model_tobit_censored <- vglm(y ~ x, family = tobit(Lower = 0, Upper = 50, type.fitted = "censored"), trace = T)
model_tobit_censored %>%
summary()VGLM linear loop 1 : loglikelihood = -59.795084
VGLM linear loop 2 : loglikelihood = -58.963179
VGLM linear loop 3 : loglikelihood = -58.94609
VGLM linear loop 4 : loglikelihood = -58.946045
VGLM linear loop 5 : loglikelihood = -58.946044
Call:
vglm(formula = y ~ x, family = tobit(Lower = 0, Upper = 50, type.fitted = "censored"),
trace = T)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept):1 -25.09608 0.49066 -51.148 <0.0000000000000002 ***
(Intercept):2 -0.09271 0.10614 -0.874 0.382
x 2.02091 0.01936 104.403 <0.0000000000000002 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Names of linear predictors: mu, loglink(sd)
Log-likelihood: -58.946 on 197 degrees of freedom
Number of Fisher scoring iterations: 5
Warning: Hauck-Donner effect detected in the following estimate(s):
'(Intercept):1'打ち切りなしの最尤推定
# 打ち切りなしの最尤推定
model_tobit_uncensored <- vglm(y ~ x, family = tobit(Lower = -Inf, Upper = Inf, type.fitted = "uncensored"), trace = T)
model_tobit_uncensored %>%
summary()VGLM linear loop 1 : loglikelihood = -298.80209
VGLM linear loop 2 : loglikelihood = -297.19837
VGLM linear loop 3 : loglikelihood = -297.17209
VGLM linear loop 4 : loglikelihood = -297.17209
VGLM linear loop 5 : loglikelihood = -297.17209
Call:
vglm(formula = y ~ x, family = tobit(Lower = -Inf, Upper = Inf,
type.fitted = "uncensored"), trace = T)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept):1 -9.35191 0.88801 -10.53 <0.0000000000000002 ***
(Intercept):2 1.55278 0.07071 21.96 <0.0000000000000002 ***
x 1.37773 0.03219 42.80 <0.0000000000000002 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Names of linear predictors: mu, loglink(sd)
Log-likelihood: -297.1721 on 197 degrees of freedom
Number of Fisher scoring iterations: 5
No Hauck-Donner effect found in any of the estimates最小二乗法による線形回帰
# 最小二乗法による線形回帰
model_ols <- lm(y ~ x)
model_ols %>%
summary()
Call:
lm(formula = y ~ x)
Residuals:
Min 1Q Median 3Q Max
-9.2938 -3.8934 0.2396 3.6403 9.2993
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -9.35191 0.89703 -10.43 <0.0000000000000002 ***
x 1.37773 0.03252 42.37 <0.0000000000000002 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 4.773 on 98 degrees of freedom
Multiple R-squared: 0.9482, Adjusted R-squared: 0.9477
F-statistic: 1795 on 1 and 98 DF, p-value: < 0.00000000000000022結果の散布図と回帰直線
トービット・モデル
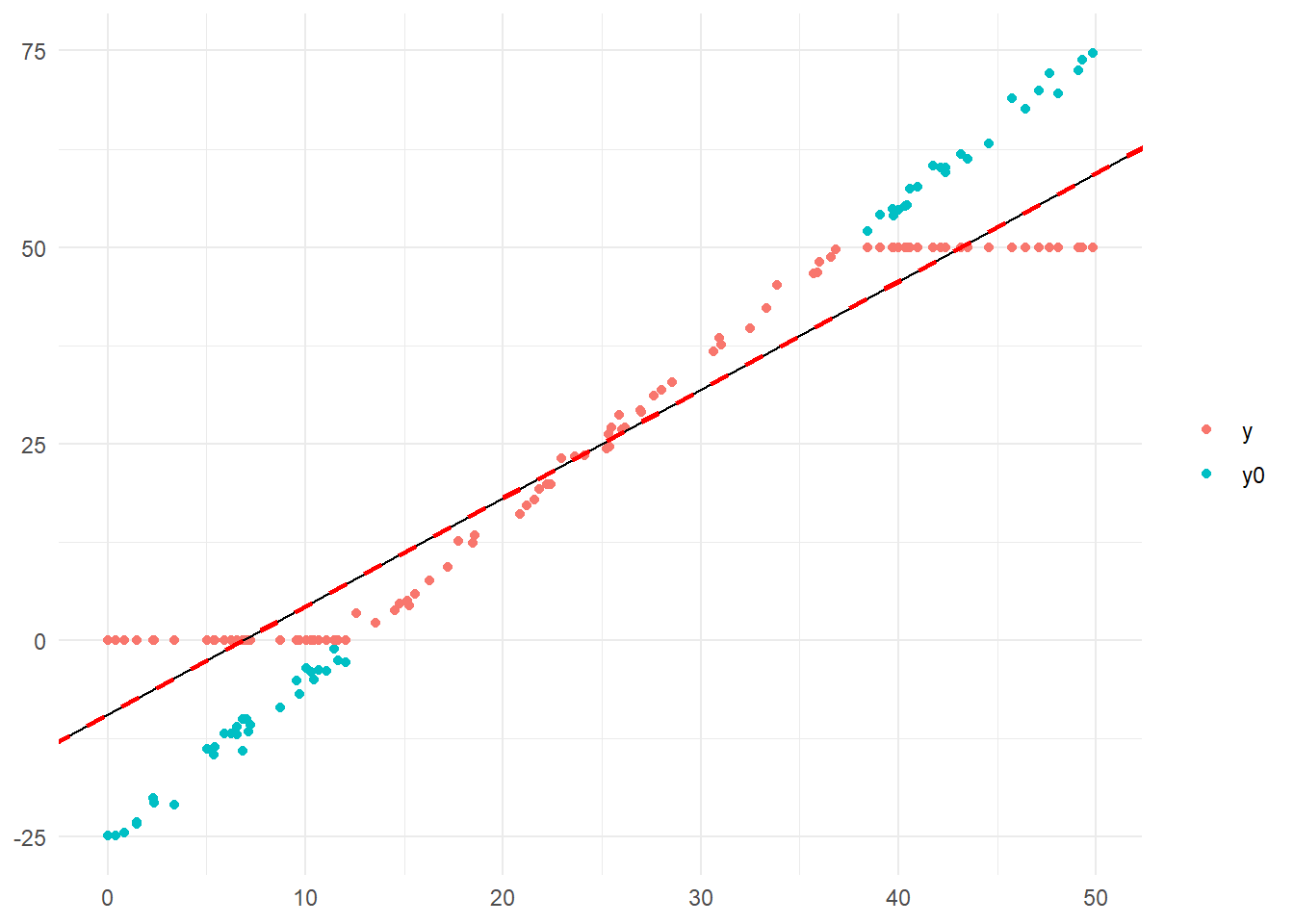
最小二乗法による線形回帰と打ち切りなしの最尤推定
参考引用資料
最終更新
Sys.time()[1] "2024-03-25 08:31:00 JST"R、Quarto、Package
R.Version()$version.string[1] "R version 4.3.3 (2024-02-29 ucrt)"quarto::quarto_version()[1] '1.4.542'packageVersion(pkg = "tidyverse")[1] '2.0.0'