Rで確率･統計:チェビシェフの不等式

Rでデータサイエンス

チェビシェフの不等式

証明

確率変数\(X=\left\{x_1,x_2\cdots,x_n\right\}\)、対応する確率を\(P=\left\{p_1,p_2,\cdots,p_n\right\}\)、\(E\left[X\right]=\mu\)、分散\(V\left[X\right]=\sigma^2\)、\(k>0\)としたとき

\[\begin{aligned}\sigma^2&=E\left[\left(X-\mu\right)^2\right]\\ &=\sum\limits_k\left(x_k-\mu\right)^2p_k\\ &=\sum\limits_{|x_k-\mu|<k\sigma}\left(x_k-\mu\right)^2p_k+\sum\limits_{|x_k-\mu|\geq k\sigma}\left(x_k-\mu\right)^2p_k\\ &\geq \sum\limits_{|x_k-\mu|\geq k\sigma}\left(x_k-\mu\right)^2p_k\\ &= \sum\limits_{|x_k-\mu|\geq k\sigma}\left|x_k-\mu\right|^2p_k\\ &\geq \sum\limits_{|x_k-\mu|\geq k\sigma}k^2\sigma^2p_k\quad\cdots\,\,\because|x_k-\mu|\geq k\sigma\\ &= k^2\sigma^2\sum\limits_{|x_k-\mu|\geq k\sigma}p_k\\&=k^2\sigma^2P\left(|X-\mu|\geq k\sigma\right)\end{aligned}\]

よって\(\sigma^2 \geq k^2\sigma^2P\left(|X-\mu|\geq k\sigma\right)\)より\[\dfrac{1}{k^2}\geq P\left(|X-\mu|\geq k\sigma\right)\]

これは\(X\)の平均\(\mu\)との差の絶対値が、標準偏差\(\sigma\)の\(k\)倍以上になる確率は\(\dfrac{1}{k^2}\)以下になることを意味し、これは離散分布でも連続分布でも成立する。

library(dplyr)
func_Chebyshev_inequality_for_normal <- function(k, sigma) {
    P <- pnorm(q = k * sigma, mean = 0, sd = sigma, lower.tail = F) * 2
    k2_reciprocal <- 1/k^2
    return(list(P = P, k2_reciprocal = k2_reciprocal))
}
# sigma = 1(標準正規分布)の場合
library(tidyr)
library(ggplot2)
df <- data.frame()
cnt <- 1
for (k in seq(0.1, 20, 0.01)) {
    result <- func_Chebyshev_inequality_for_normal(k = k, sigma = 1)
    P <- result$P
    k2_reciprocal <- result$k2_reciprocal
    df[cnt, 1] <- cnt
    df[cnt, 2] <- P
    df[cnt, 3] <- k2_reciprocal
    cnt <- cnt + 1
}
colnames(df) <- c("N", "P", "k2_reciprocal")
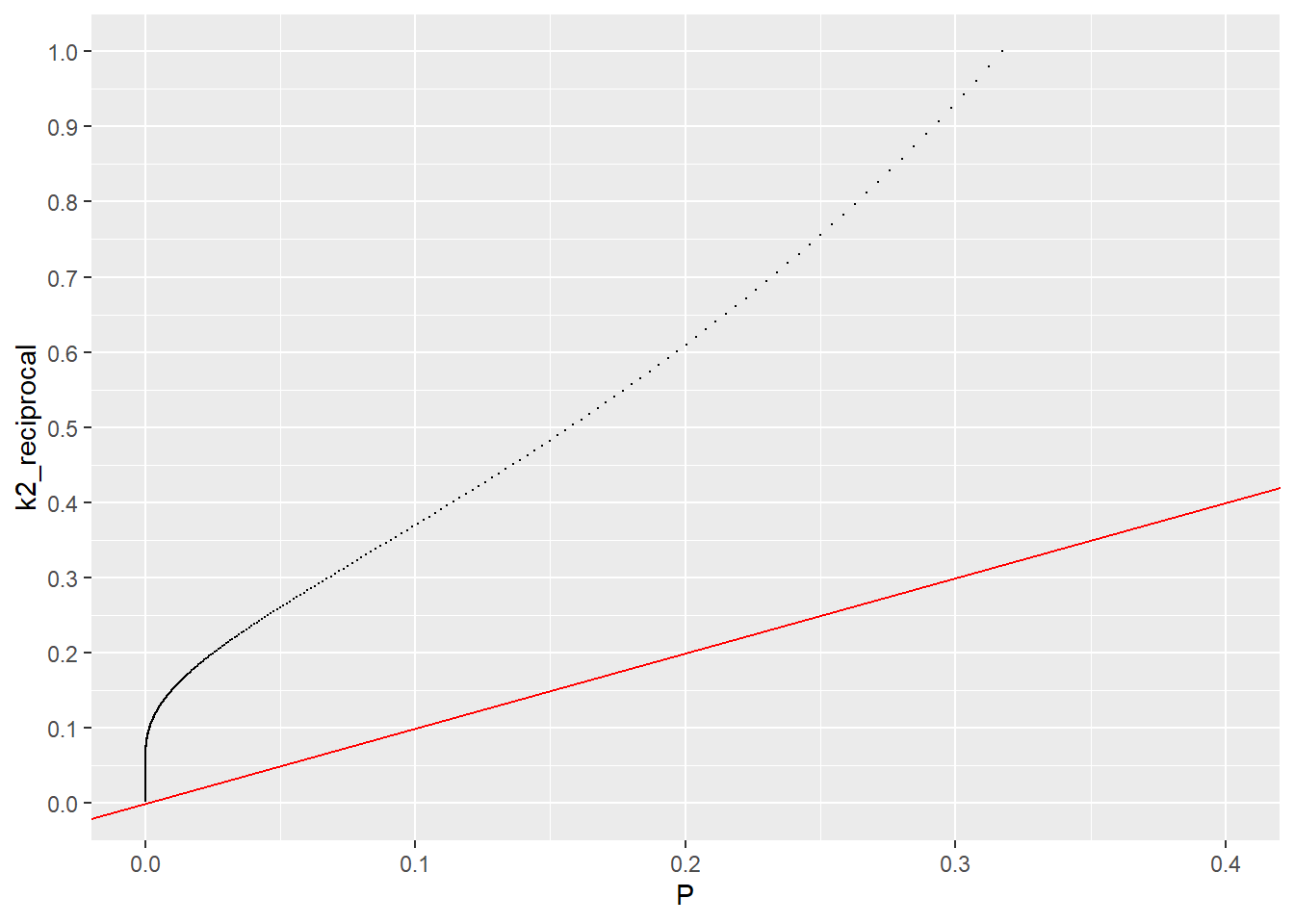
g0 <- ggplot(data = df, mapping = aes(x = P, y = k2_reciprocal))
g0 + geom_point(size = 0.1) + geom_abline(slope = 1, intercept = 0, col = "red") + xlim(0, 0.4) + scale_y_continuous(breaks = seq(0, 1, 0.1), limits = c(0, 1))
Figure 1 
# 参考
integrate(f = "dnorm", lower = -Inf, upper = -1.96)
0.0249979 with absolute error < 0.000019

参考引用資料

最終更新

Sys.time()
[1] "2024-04-14 14:08:14 JST"

R、Quarto、Package

R.Version()$version.string
[1] "R version 4.3.3 (2024-02-29 ucrt)"
quarto::quarto_version()
[1] '1.4.542'
packageVersion(pkg = "tidyverse")
[1] '2.0.0'

著者