Rで確率･統計:一致推定量

Rでデータサイエンス

一致推定量

単回帰モデルを\[Y_i=\alpha+\beta X_i+u_i,\quad i=1,2,\cdots,n\]として、以下の仮定を置く。

  1. \(\mathrm{E}(u_i)=0\)
  2. \(\mathrm{V}(u_i)=\mathrm{E}(u_i^2)=\sigma_i^2\quad\cdots\)不均一分散
  3. \(i\neq j\)の場合、\(\mathrm{Cov}(u_i,u_j)=\mathrm{E}(u_iu_j)=0\quad\cdots\)系列相関なし

最小二乗推定量は\[\hat{\beta}=\displaystyle\sum_{i=1}^n\dfrac{X_i-\bar{X}}{\displaystyle\sum_{j=1}^n\left(X_j-\bar{X}\right)^2}\cdot Y_i\]

ここで\[\omega_i=\dfrac{X_i-\bar{X}}{\displaystyle\sum_{j=1}^n\left(X_j-\bar{X}\right)^2}\]とすると、\[\hat{\beta}=\displaystyle\sum_{i=1}^n\omega_i\,Y_i=\beta+\displaystyle\sum_{i=1}^n\omega_i\,u_i\]

\(X_i\)は非確率変数であるため、推定量の期待値は\[\mathrm{E}\left(\hat{\beta}\right)=\mathrm{E}\left(\beta+\displaystyle\sum_{i=1}^n\omega_i\,u_i\right)=\mathrm{E}(\beta)+\mathrm{E}\left(\displaystyle\sum_{i=1}^n\omega_i\,u_i\right)=\beta+\displaystyle\sum_{i=1}^n\omega_i\,\mathrm{E}(u_i)=\beta+\displaystyle\sum_{i=1}^n\omega_i\cdot0=\beta\]

つまり誤差項\(u_1,u_2,\cdots,u_n\)が分散不均一であっても、\(\hat{\beta}\)は不偏推定量となる。

なお、\(\beta\)の推定量は\[\begin{aligned} \hat{\beta} &=\dfrac{S_{xy}}{S_{xx}} =\dfrac{\displaystyle\sum_{i=1}^n\left(X_i-\bar{X}\right)\left(Y_i-\bar{Y}\right)}{\displaystyle\sum_{i=1}^n\left(X_i-\bar{X}\right)^2} =\dfrac{\displaystyle\sum_{i=1}^n\left(X_i-\bar{X}\right)\left(\beta\left(X_i-\bar{X}\right)+(u_i-\bar{u})\right)}{\displaystyle\sum_{i=1}^n\left(X_i-\bar{X}\right)^2} \\&=\dfrac{\displaystyle\sum_{i=1}^n\left(X_i-\bar{X}\right)\left(\beta\left(X_i-\bar{X}\right)\right)}{\displaystyle\sum_{i=1}^n\left(X_i-\bar{X}\right)^2}+\dfrac{\displaystyle\sum_{i=1}^n\left(X_i-\bar{X}\right)\left(u_i-\bar{u}\right)}{\displaystyle\sum_{i=1}^n\left(X_i-\bar{X}\right)^2} \\&=\beta+\dfrac{\displaystyle\sum_{i=1}^n\left(X_i-\bar{X}\right)\left(u_i-\bar{u}\right)}{\displaystyle\sum_{i=1}^n\left(X_i-\bar{X}\right)^2} =\beta+\dfrac{\displaystyle\sum_{i=1}^n\left(X_i-\bar{X}\right)u_i-\displaystyle\sum_{i=1}^n\left(X_i-\bar{X}\right)\bar{u}}{\displaystyle\sum_{i=1}^n\left(X_i-\bar{X}\right)^2} \\&=\beta+\dfrac{\displaystyle\sum_{i=1}^n\left(X_i-\bar{X}\right)u_i-\displaystyle\sum_{i=1}^n\left(X_i-\bar{X}\right)\displaystyle\sum_{i=1}^n\bar{u}}{\displaystyle\sum_{i=1}^n\left(X_i-\bar{X}\right)^2}=\beta+\dfrac{\displaystyle\sum_{i=1}^n\left(X_i-\bar{X}\right)u_i-\displaystyle\sum_{i=1}^n\left(X_i-\bar{X}\right)\cdot0}{\displaystyle\sum_{i=1}^n\left(X_i-\bar{X}\right)^2} =\beta+\dfrac{\displaystyle\sum_{i=1}^n\left(X_i-\bar{X}\right)u_i}{\displaystyle\sum_{i=1}^n\left(X_i-\bar{X}\right)^2}\\&=\beta+\displaystyle\sum_{i=1}^n\omega_iu_i\end{aligned}\]

但し\[\omega_i=\dfrac{\left(X_i-\bar{X}\right)}{\displaystyle\sum_{i=1}^n\left(X_i-\bar{X}\right)^2}\]

\(X\)が非確率変数であることから\(\omega\)も非確率変数であり、前述の通り\(\mathrm{E}(u_i)=0,\,\mathrm{E}(u_i^2)=\sigma^2,\,\mathrm{Cov}(u_i,\,u_j)=\mathrm{E}(u_i\,u_j)=0\)を仮定しているので、推定量の分散は\[\begin{aligned} V(\hat{\beta})&=E\left(\hat{\beta}-E\left(\hat{\beta}\right)\right)^2=E\left(\hat{\beta}-\beta\right)^2 \\&=E\left(\displaystyle\sum_{i=1}^n\omega_iu_i\right)^2=E\left(\displaystyle\sum_{i=1}^n\omega_i^2\,u_i^2+\displaystyle\sum_{i\neq j}\omega_i\,\omega_j\,u_i\,u_j\right) \\&=\displaystyle\sum_{i=1}^n\omega_i^2E\left(u_i^2\right)+\displaystyle\sum_{i\neq j}\omega_i\,\omega_j\,E\left(u_i\,u_j\right)=\displaystyle\sum_{i=1}^n\omega_i^2\sigma^2+\displaystyle\sum_{i\neq j}\omega_i\omega_j\cdot 0=\sigma^2\displaystyle\sum_{i=1}^n\omega_i^2 \\&=\sigma^2\displaystyle\sum_{i=1}^n\left(\dfrac{X_i-\bar{X}}{\displaystyle\sum_{i=1}^n\left(X_i-\bar{X}\right)^2}\right)^2 =\sigma^2\dfrac{\left(X_1-\bar{X}\right)^2+\left(X_2-\bar{X}\right)^2\cdots\left(X_n-\bar{X}\right)^2}{\left(\left(X_1-\bar{X}\right)^2+\left(X_2-\bar{X}\right)^2\cdots\left(X_n-\bar{X}\right)^2\right)^2} \\&=\dfrac{\sigma^2}{\displaystyle\sum_{i=1}^n\left(X_i-\bar{X}\right)^2}=\dfrac{\sigma^2}{n\cdot V(X)} \end{aligned}\]

よって\(n\rightarrow\infty\)のとき、\[V(\hat{\beta})\rightarrow0\]となるため、\(\hat{\beta}\)は\(\beta\)の一致推定量となる。

library(dplyr)
func_lm_sim <- function(n, b, u_coef) {
    u <- vector()
    u[1] <- rnorm(1)
    for (i in 2:n) {
        u[i] <- u_coef * u[i - 1] + rnorm(1, sd = 0.1)  # 誤差項に系列相関あり
    }
    x <- runif(n = n)
    y <- b * x + u
    b_hat <- lm(y ~ x - 1) %>%
        summary() %>%
        {
            .$coef[1]
        }
    return(b_hat)
}
b <- 0.7
u_coef <- 0.7
rep <- 500
# シミュレーション 1
sim_bhat <- vector()
n <- 30
for (i in seq(rep)) {
    sim_bhat[i] <- func_lm_sim(n = n, b = b, u_coef = u_coef)
}
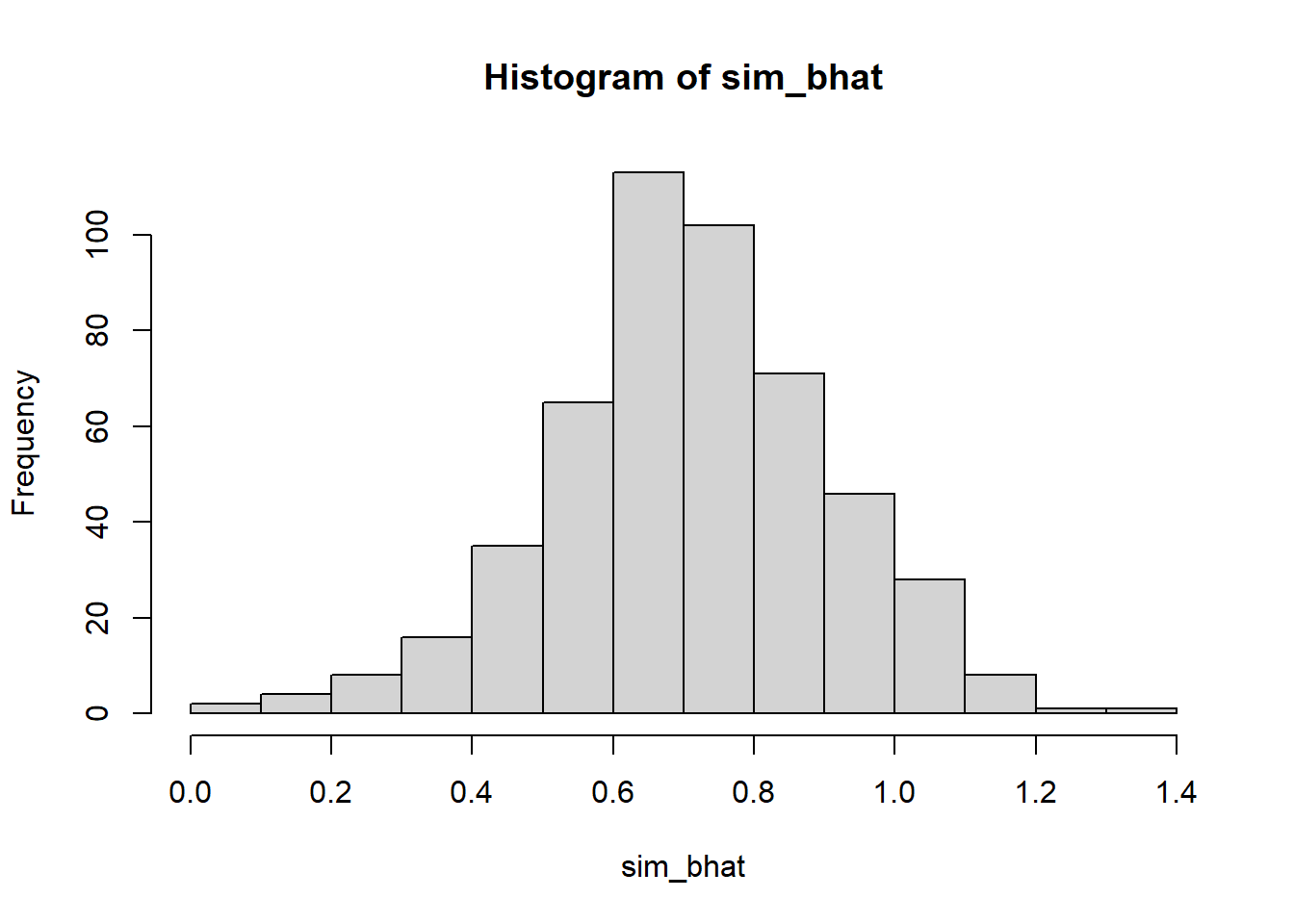
hist(sim_bhat)
summary(sim_bhat)
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
0.01276 0.59666 0.70526 0.70998 0.83637 1.32648
Figure 1 
# シミュレーション 2
sim_bhat <- vector()
n <- 300
for (i in seq(rep)) {
    sim_bhat[i] <- func_lm_sim(n = n, b = b, u_coef = u_coef)
}
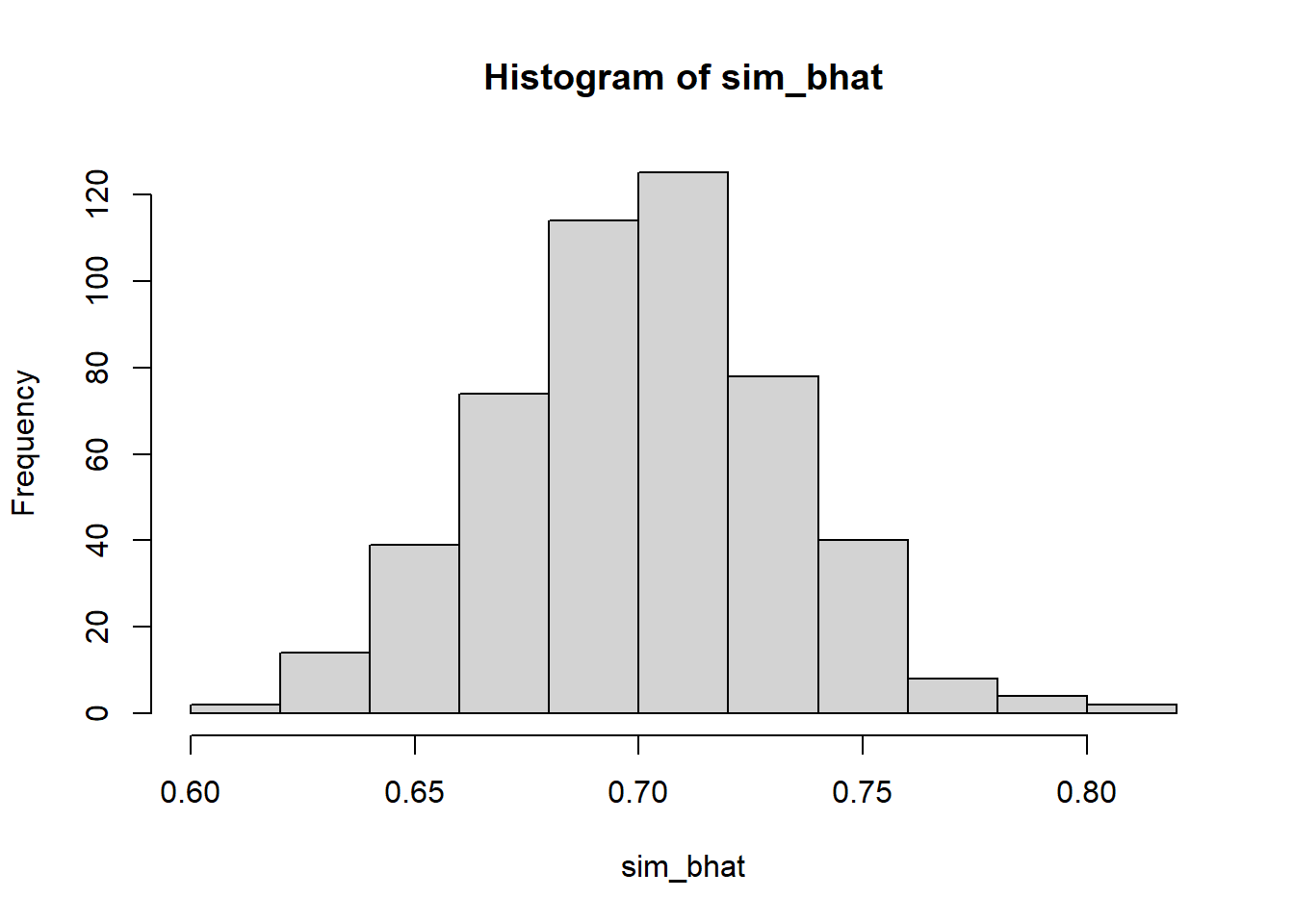
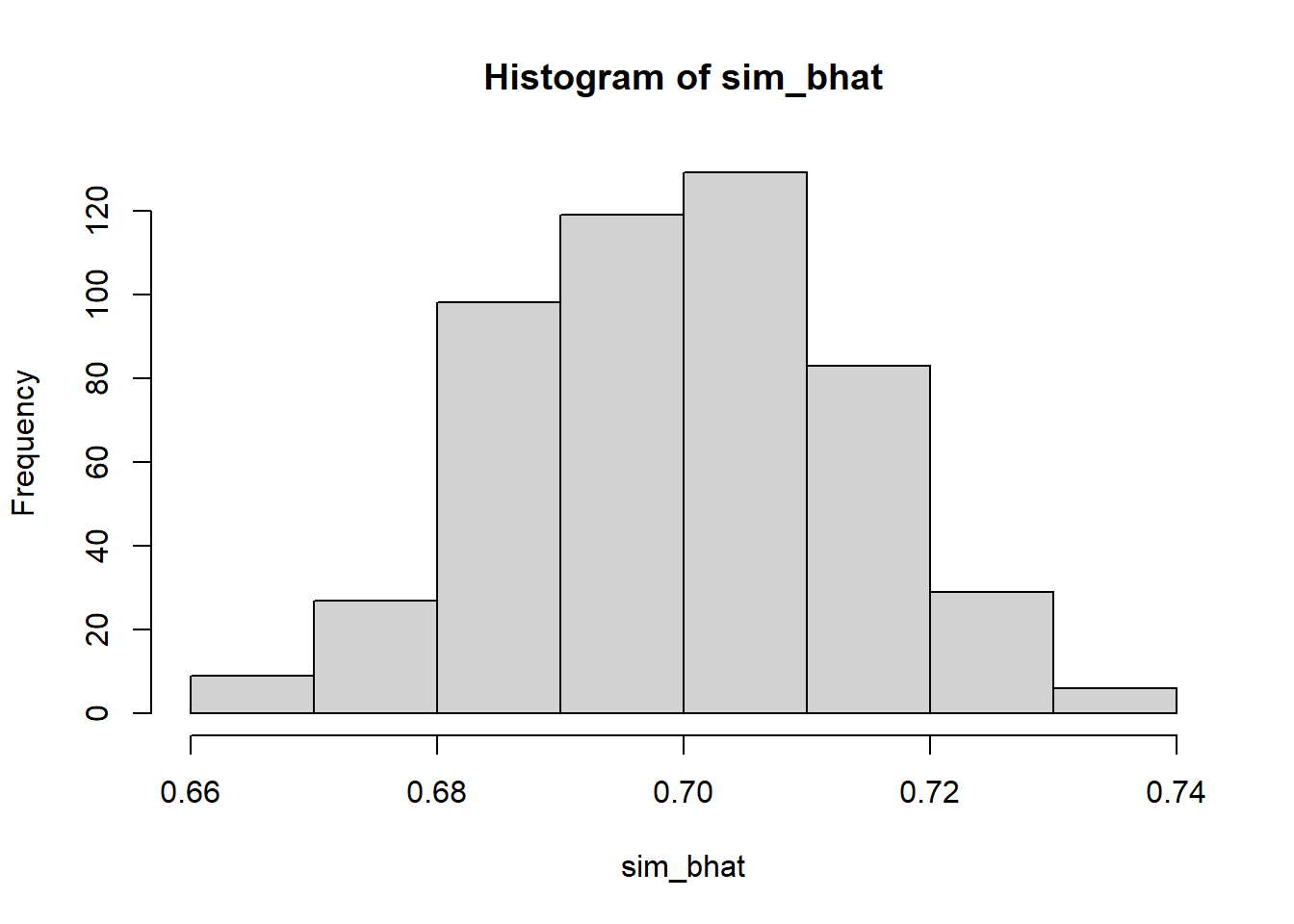
hist(sim_bhat)
summary(sim_bhat)
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
 0.6113  0.6798  0.7013  0.7006  0.7220  0.8146
Figure 2 
# シミュレーション 3
sim_bhat <- vector()
n <- 1500
for (i in seq(rep)) {
    sim_bhat[i] <- func_lm_sim(n = n, b = b, u_coef = u_coef)
}
hist(sim_bhat)
summary(sim_bhat)
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
 0.6635  0.6894  0.6998  0.6996  0.7095  0.7360
Figure 3

参考引用資料

最終更新

Sys.time()
[1] "2024-04-14 14:31:58 JST"

R、Quarto、Package

R.Version()$version.string
[1] "R version 4.3.3 (2024-02-29 ucrt)"
quarto::quarto_version()
[1] '1.4.542'
packageVersion(pkg = "tidyverse")
[1] '2.0.0'

著者