Rで確率･統計:サンプルサイズの決定:t検定の場合(2群、対応あり)

Rでデータサイエンス

サンプルサイズの決定:t検定の場合(2群、対応あり)

lapply(X = c("dplyr", "pwr", "ggplot2", "scales"), require, character.only = T)

t検定(2群、対応あり)の例

あるクラスの全員(n人)に出来事Aに関する理解度テストを行ったところ、n人の平均点は\(\mu_1\)点であった。テスト後に出来事Aの詳細を解説し、その後同一の理解度テストを行ったところn人の平均点は\(\mu_2\)であった。

  • \(\textrm{H}_0\):詳細解説前後で平均点に変化なし。
  • \(\textrm{H}_1\):詳細解説前後で平均点に変化はあった(理解度が上がった又は理解度が下がったの両側検定)。

効果量、有意水準、サンプルサイズが与えられた場合の検定力算出

\[d=\dfrac{\mu_2-\mu_1}{\sigma}\]

# 効果量の目安
effect_size <- sapply(c("small", "medium", "large"), function(x) {
    cohen.ES(test = "t", size = x)$effect.size
})
effect_size
 small medium  large 
   0.2    0.5    0.8 
# 検定力算出コードは関数から引用
# 効果量(Effect size)
# 標準偏差に対する平均値の差の寄与が 0.5
d <- 0.5
# 有意水準
sig.level <- 0.05
# サンプルサイズ
n <- 40
# 検定タイプ
type <- "paired"
alternative <- "two.sided"
tsample <- switch(type, one.sample = 1, two.sample = 2, paired = 1)
tside <- switch(alternative, less = 1, two.sided = 2, greater = 1)
# 自由度
nu <- (n - 1) * tsample
nu
[1] 39
# 自由度 nu のt分布における、境界点(両側) sig.level/2 に対応するt値
qu <- qt(sig.level/tside, nu, lower = FALSE)
qu
[1] 2.022691
# 自由度 nu の非心t分布における検定統計量(qu)に対する上側確率
p_upper <- pt(qu, nu, ncp = sqrt(n/tsample) * d, lower = FALSE)
p_upper
[1] 0.8693979
# 自由度 nu の非心t分布における検定統計量(-qu)に対する下側確率
p_lower <- pt(-qu, nu, ncp = sqrt(n/tsample) * d, lower = TRUE)
p_lower
[1] 0.0000002238158
# 両者の合計
power <- p_upper + p_lower
power
[1] 0.8693981

よって、対立仮説が正しく、かつ帰無仮説が棄却される確率は86.94`%

# 改めて関数で検定力を確認
result <- pwr.t.test(d = d, sig.level = sig.level, n = n, type = type, alternative = alternative)
result
{
    result %>%
        plot()
} + geom_hline(yintercept = 0.8) + scale_x_continuous(breaks = pretty_breaks(n = 10)) + scale_y_continuous(breaks = pretty_breaks(n = 10), labels = function(x) paste0(x * 100, "%"))

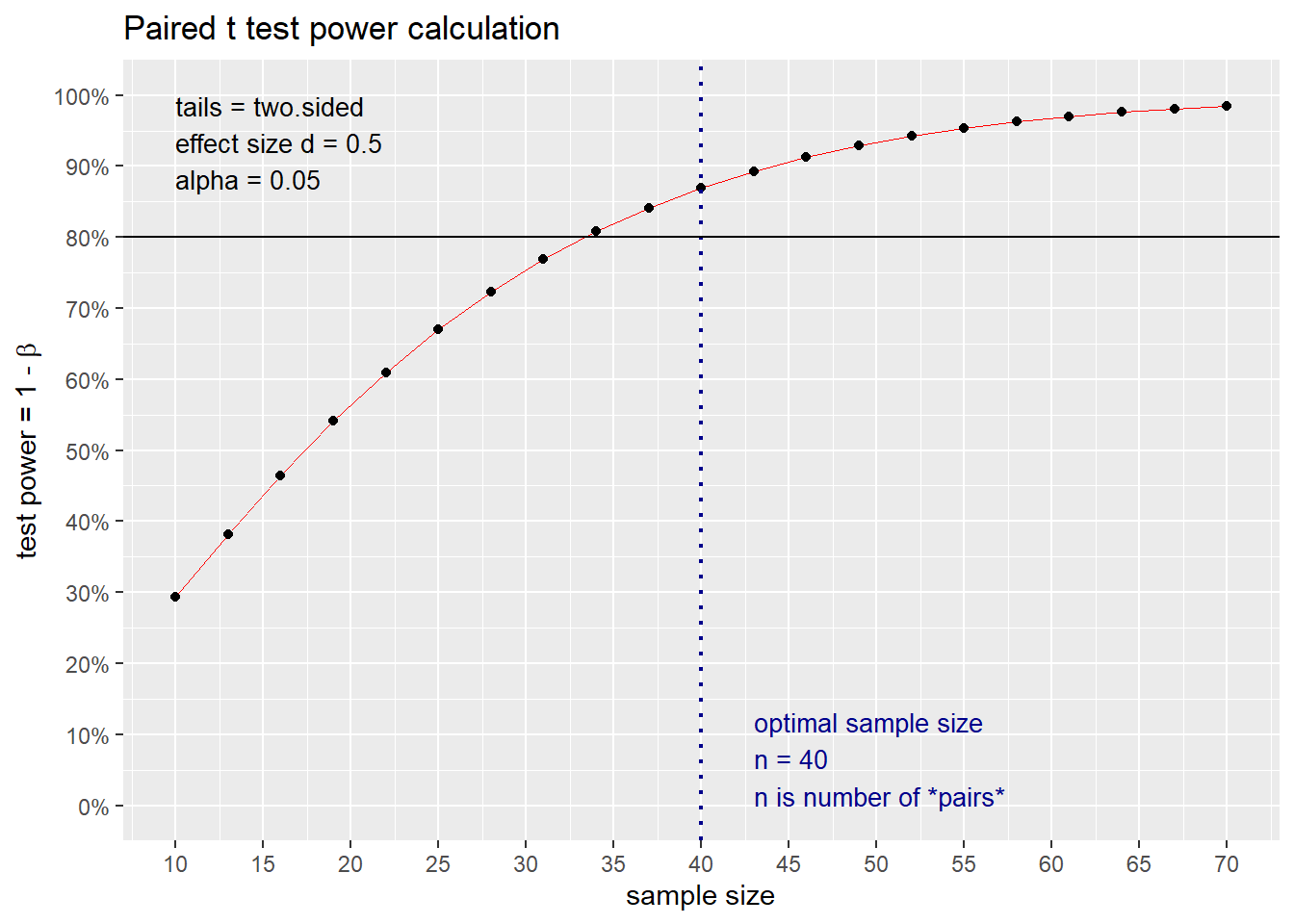
     Paired t test power calculation 

              n = 40
              d = 0.5
      sig.level = 0.05
          power = 0.8693981
    alternative = two.sided

NOTE: n is number of *pairs*
Figure 1

なお、pwr.t.test 関数では効果量、有意水準および検定力が与えられた場合、サンプルサイズ n を 2 + 1e-10 から 1e+09 の範囲として求めた検定力と与えられた検定力との差がゼロになる n をニュートン法により求めている。

# n <- uniroot(function(n) eval(p.body) - power, c(2 + 1e-10, 1e+09))$root

参考引用資料

最終更新

Sys.time()
[1] "2024-04-19 08:42:23 JST"

R、Quarto、Package

R.Version()$version.string
[1] "R version 4.3.3 (2024-02-29 ucrt)"
quarto::quarto_version()
[1] '1.4.553'
packageVersion(pkg = "tidyverse")
[1] '2.0.0'

著者