Rで時系列分析:共和分検定

Rでデータサイエンス

共和分検定

共和分ベクトルと誤差修正項

\(x_t,y_t\)いすれも\(I(1)\)である2変数のVARモデルを考える。ここではラグを2期とし、誤差項\(\epsilon_t,\eta_t\)は独立同一正規分布に従うと仮定する。

\[ \begin{bmatrix}x_t\\y_t\end{bmatrix}=\begin{bmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{bmatrix}\begin{bmatrix}x_{t-1}\\y_{t-1}\end{bmatrix}+\begin{bmatrix}b_{11}&b_{12}\\b_{21}&b_{22}\end{bmatrix}\begin{bmatrix}x_{t-2}\\y_{t-2}\end{bmatrix}+\begin{bmatrix}\mu_x\\\mu_y\end{bmatrix}+\begin{bmatrix}\epsilon_t\\\eta_t\end{bmatrix} \]

\(x_t,y_t\)は\(I(1)\)であるため一階差分系列は定常時系列となる。\[\begin{bmatrix}x_t\\y_t\end{bmatrix}-\begin{bmatrix}x_{t-1}\\y_{t-1}\end{bmatrix}=\begin{bmatrix}\Delta x_t\\\Delta y_t\end{bmatrix}\]

右辺は以下の通り。

\[ \begin{bmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{bmatrix}\begin{bmatrix}x_{t-1}\\y_{t-1}\end{bmatrix}+\begin{bmatrix}b_{11}&b_{12}\\b_{21}&b_{22}\end{bmatrix}\begin{bmatrix}x_{t-2}\\y_{t-2}\end{bmatrix}+\begin{bmatrix}\mu_x\\\mu_y\end{bmatrix}+\begin{bmatrix}\epsilon_t\\\eta_t\end{bmatrix}-\begin{bmatrix}x_{t-1}\\y_{t-1}\end{bmatrix} \]

ここで\[\Pi_1=\begin{bmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{bmatrix}\quad\Pi_2=\begin{bmatrix}b_{11}&b_{12}\\b_{21}&b_{22}\end{bmatrix}\quad\Gamma=\Pi_1-\mathrm{I}\quad\Pi=\mathrm{I}-\Pi_1-\Pi_2\]として以下の通りに右辺を変形する。

\[ \begin{aligned} \begin{bmatrix}\Delta x_t\\\Delta y_t\end{bmatrix}=&\Pi_1\begin{bmatrix}x_{t-1}\\y_{t-1}\end{bmatrix}+\Pi_2\begin{bmatrix}x_{t-2}\\y_{t-2}\end{bmatrix}+\begin{bmatrix}\mu_x\\\mu_y\end{bmatrix}+\begin{bmatrix}\epsilon_t\\\eta_t\end{bmatrix}-\mathrm{I}\begin{bmatrix}x_{t-1}\\y_{t-1}\end{bmatrix}\\ =&\Pi_1\begin{bmatrix}x_{t-1}\\y_{t-1}\end{bmatrix}+\Pi_2\begin{bmatrix}x_{t-2}\\y_{t-2}\end{bmatrix}+\begin{bmatrix}\mu_x\\\mu_y\end{bmatrix}+\begin{bmatrix}\epsilon_t\\\eta_t\end{bmatrix}-\mathrm{I}\begin{bmatrix}x_{t-1}\\y_{t-1}\end{bmatrix}-\Pi_1\begin{bmatrix}x_{t-2}\\y_{t-2}\end{bmatrix}+\Pi_1\begin{bmatrix}x_{t-2}\\y_{t-2}\end{bmatrix}-\mathrm{I}\begin{bmatrix}x_{t-2}\\y_{t-2}\end{bmatrix}+\mathrm{I}\begin{bmatrix}x_{t-2}\\y_{t-2}\end{bmatrix}\\ =&\Pi_1\begin{bmatrix}x_{t-1}\\y_{t-1}\end{bmatrix}-\mathrm{I}\begin{bmatrix}x_{t-1}\\y_{t-1}\end{bmatrix}-\Pi_1\begin{bmatrix}x_{t-2}\\y_{t-2}\end{bmatrix}+\mathrm{I}\begin{bmatrix}x_{t-2}\\y_{t-2}\end{bmatrix}+\Pi_2\begin{bmatrix}x_{t-2}\\y_{t-2}\end{bmatrix}+\begin{bmatrix}\mu_x\\\mu_y\end{bmatrix}+\begin{bmatrix}\epsilon_t\\\eta_t\end{bmatrix}+\Pi_1\begin{bmatrix}x_{t-2}\\y_{t-2}\end{bmatrix}-\mathrm{I}\begin{bmatrix}x_{t-2}\\y_{t-2}\end{bmatrix}\\ =&(\Pi_1-\mathrm{I})\begin{bmatrix}x_{t-1}\\y_{t-1}\end{bmatrix}-(\Pi_1-\mathrm{I})\begin{bmatrix}x_{t-2}\\y_{t-2}\end{bmatrix}-\mathrm{I}\begin{bmatrix}x_{t-2}\\y_{t-2}\end{bmatrix}+\Pi_1\begin{bmatrix}x_{t-2}\\y_{t-2}\end{bmatrix}+\Pi_2\begin{bmatrix}x_{t-2}\\y_{t-2}\end{bmatrix}+\begin{bmatrix}\mu_x\\\mu_y\end{bmatrix}+\begin{bmatrix}\epsilon_t\\\eta_t\end{bmatrix}\\ =&(\Pi_1-\mathrm{I})(\begin{bmatrix}x_{t-1}\\y_{t-1}\end{bmatrix}-\begin{bmatrix}x_{t-2}\\y_{t-2}\end{bmatrix})-\mathrm{I}\begin{bmatrix}x_{t-2}\\y_{t-2}\end{bmatrix}+\Pi_1\begin{bmatrix}x_{t-2}\\y_{t-2}\end{bmatrix}+\Pi_2\begin{bmatrix}x_{t-2}\\y_{t-2}\end{bmatrix}+\begin{bmatrix}\mu_x\\\mu_y\end{bmatrix}+\begin{bmatrix}\epsilon_t\\\eta_t\end{bmatrix}\\ =&(\Pi_1-\mathrm{I})\begin{bmatrix}\Delta x_{t-1}\\\Delta y_{t-1}\end{bmatrix}-\mathrm{I}\begin{bmatrix}x_{t-2}\\y_{t-2}\end{bmatrix}+\Pi_1\begin{bmatrix}x_{t-2}\\y_{t-2}\end{bmatrix}+\Pi_2\begin{bmatrix}x_{t-2}\\y_{t-2}\end{bmatrix}+\begin{bmatrix}\mu_x\\\mu_y\end{bmatrix}+\begin{bmatrix}\epsilon_t\\\eta_t\end{bmatrix}\\ =&(\Pi_1-\mathrm{I})\begin{bmatrix}\Delta x_{t-1}\\\Delta y_{t-1}\end{bmatrix}-\left(\mathrm{I}\begin{bmatrix}x_{t-2}\\y_{t-2}\end{bmatrix}-\Pi_1\begin{bmatrix}x_{t-2}\\y_{t-2}\end{bmatrix}-\Pi_2\begin{bmatrix}x_{t-2}\\y_{t-2}\end{bmatrix}\right)+\begin{bmatrix}\mu_x\\\mu_y\end{bmatrix}+\begin{bmatrix}\epsilon_t\\\eta_t\end{bmatrix}\\ =&(\Pi_1-\mathrm{I})\begin{bmatrix}\Delta x_{t-1}\\\Delta y_{t-1}\end{bmatrix}-(\mathrm{I} -\Pi_1-\Pi_2)\begin{bmatrix}x_{t-2}\\y_{t-2}\end{bmatrix}+\begin{bmatrix}\mu_x\\\mu_y\end{bmatrix}+\begin{bmatrix}\epsilon_t\\\eta_t\end{bmatrix}\\ =&\Gamma\begin{bmatrix}\Delta x_{t-1}\\\Delta y_{t-1}\end{bmatrix}-\Pi\begin{bmatrix}x_{t-2}\\y_{t-2}\end{bmatrix}+\begin{bmatrix}\mu_x\\\mu_y\end{bmatrix}+\begin{bmatrix}\epsilon_t\\\eta_t\end{bmatrix}\\ \end{aligned} \]

\(I(1)\)の一階差分ですので右辺も当然に定常。第3項は定数項、第1項および第4項は定常ですので第2項も定常でなければならない。ところが\(\begin{bmatrix}x_{t-2}&y_{t-2}\end{bmatrix}^t\)は非定常であるため

1. \(\Pi\)がゼロ行列
2. \(\Pi\)と\(\begin{bmatrix}x_{t-2}&y_{t-2}\end{bmatrix}^t\)との積のベクトルの各成分が定常

のいずれか。

1の場合は\(x_t,y_t\)は1次独立な非定常変数であり共和分が存在しない。
2の場合は\(x_{t-2},y_{t-2}\)の線形結合は定常性を満たしており共和分関係あり。さらに第2項はGrangerの表現定理により以下の通りに分解できる。

\[\Pi\begin{bmatrix}x_{t-2}\\y_{t-2}\end{bmatrix}=\begin{bmatrix}\alpha_1\\\alpha_2\end{bmatrix}\left(\beta_1,\beta_2\right)\begin{bmatrix}x_{t-2}\\y_{t-2}\end{bmatrix}=\begin{bmatrix}\alpha_1\cdot EC_{t-2}\\\alpha_2\cdot EC_{t-2}\end{bmatrix}\]ここで\(EC_{t-2}=\beta_1x_{t-2}\)であり代入すると\[\begin{bmatrix}\Delta x_t\\\Delta y_t\end{bmatrix}=\Gamma\begin{bmatrix}\Delta x_{t-1}\\\Delta y_{t-1}\end{bmatrix}-\begin{bmatrix}\alpha_1\cdot EC_{t-2}\\\alpha_2\cdot EC_{t-2}\end{bmatrix}+\begin{bmatrix}\mu_x\\\mu_y\end{bmatrix}+\begin{bmatrix}\epsilon_t\\\eta_t\end{bmatrix}\]

線形結合\(EC_t=\beta_1x_t+\beta_2y_t\)が定常とみなせる場合、ベクトル\(\left(\beta_1,\beta_2\right)\)を共和分ベクトルといい、\(EC_{t-2}\)を誤差修正項(Error Correction Term)と呼ぶ。

参考引用資料

• https://www.imes.boj.or.jp/research/papers/japanese/kk11-2-4.pdf

---

全くもって無駄極まりない作業ですが展開してみました。

右辺第1項 \[ \begin{aligned} &\Gamma\begin{bmatrix}\Delta x_{t-1}\\\Delta y_{t-1}\end{bmatrix}\\ &=\left(\Pi_1-\mathrm{I}\right)\begin{bmatrix}\Delta x_{t-1}\\\Delta y_{t-1}\end{bmatrix}\\ &=\begin{bmatrix}a_{11}-1&a_{12}\\a_{21}&a_{22}-1\end{bmatrix}\begin{bmatrix}\Delta x_{t-1}\\\Delta y_{t-1}\end{bmatrix}\\ &=\begin{bmatrix}(a_{11}-1)\Delta x_{t-1}+a_{12}\Delta y_{t-1}\\a_{21}\Delta x_{t-1}+(a_{22}-1)\Delta y_{t-1}\end{bmatrix}=\begin{bmatrix}a_{11}\Delta x_{t-1}-\Delta x_{t-1}+a_{12}\Delta y_{t-1}\\a_{21}\Delta x_{t-1}+a_{22}\Delta y_{t-1}-\Delta y_{t-1}\end{bmatrix}\\ &=\begin{bmatrix}a_{11}x_{t-1}-a_{11}x_{t-2}-x_{t-1}+x_{t-2}+a_{12}y_{t-1}-a_{12}y_{t-2}\\a_{21}x_{t-1}-a_{21}x_{t-2}+a_{22}y_{t-1}-a_{22}y_{t-2}-y_{t-1}+y_{t-2}\end{bmatrix} \end{aligned} \]

右辺第2項 \[ \begin{aligned} &\Pi\begin{bmatrix}x_{t-2}\\y_{t-2}\end{bmatrix}\\ &=\left(\mathrm{I}-\Pi_1-\Pi_2\right)\begin{bmatrix}x_{t-2}\\y_{t-2}\end{bmatrix}\\ &=\begin{bmatrix}1-a_{11}-b_{11}&-a_{12}-b_{12}\\-a_{21}-b_{21}&1-a_{22}-b_{22}\end{bmatrix}\begin{bmatrix}x_{t-2}\\y_{t-2}\end{bmatrix}\\ &=\begin{bmatrix}x_{t-2}-a_{11}x_{t-2}-b_{11}x_{t-2}-a_{12}y_{t-2}-b_{12}y_{t-2}\\-a_{21}x_{t-2}-b_{21}x_{t-2}+y_{t-2}-a_{22}y_{t-2}-b_{22}y_{t-2}\end{bmatrix} \end{aligned} \]

右辺第1項-右辺第2項 \[ \begin{aligned} &\begin{bmatrix}a_{11}x_{t-1}-a_{11}x_{t-2}-x_{t-1}+x_{t-2}+a_{12}y_{t-1}-a_{12}y_{t-2}-(x_{t-2}-a_{11}x_{t-2}-b_{11}x_{t-2}-a_{12}y_{t-2}-b_{12}y_{t-2})\\ a_{21}x_{t-1}-a_{21}x_{t-2}+a_{22}y_{t-1}-a_{22}y_{t-2}-y_{t-1}+y_{t-2} -(-a_{21}x_{t-2}-b_{21}x_{t-2}+y_{t-2}-a_{22}y_{t-2}-b_{22}y_{t-2})\end{bmatrix}\\ &=\begin{bmatrix}a_{11}x_{t-1}-a_{11}x_{t-2}-x_{t-1}+x_{t-2}+a_{12}y_{t-1}-a_{12}y_{t-2}-x_{t-2}+a_{11}x_{t-2}+b_{11}x_{t-2}+a_{12}y_{t-2}+b_{12}y_{t-2}\\ a_{21}x_{t-1}-a_{21}x_{t-2}+a_{22}y_{t-1}-a_{22}y_{t-2}-y_{t-1}+y_{t-2}+a_{21}x_{t-2}+b_{21}x_{t-2}-y_{t-2}+a_{22}y_{t-2}+b_{22}y_{t-2}\end{bmatrix}\\ &=\begin{bmatrix}a_{11}x_{t-1}+a_{12}y_{t-1}+b_{11}x_{t-2}+b_{12}y_{t-2}-x_{t-1}\\ a_{21}x_{t-1}+a_{22}y_{t-1}+b_{21}x_{t-2}+b_{22}y_{t-2}-y_{t-1}\end{bmatrix}\\ &=\begin{bmatrix}a_{11}&a_{12}\\a_{21}&a_{22}\end{bmatrix}\begin{bmatrix}x_{t-1}\\y_{t-1}\end{bmatrix}+\begin{bmatrix}b_{11}&b_{12}\\b_{21}&b_{22}\end{bmatrix}\begin{bmatrix}x_{t-2}\\y_{t-2}\end{bmatrix}-\begin{bmatrix}x_{t-1}\\y_{t-1}\end{bmatrix} \end{aligned}\\ \]

---

Example

• 有意水準は5%とする。

library(dplyr)
library(urca)
library(tidyr)
library(tibble)
library(ggplot2)
library(vars)
library(tseries)
library(egcm)

func_sample_vector <- function(p, n) {
    set.seed(20210516)
    x1 <- rnorm(n = n + p) %>%
        cumsum()
    length(x1)
    x2 <- tail(x1, length(x1) - p) + rnorm(n = length(x1) - p)
    length(x2)
    x3 <- tail(x2, length(x2) - p) + rnorm(n = length(x2) - p)
    length(x3)
    df <- sapply(list(x1, x2, x3), function(i) head(i, length(x3))) %>%
        data.frame() %>%
        add_column(.data = ., n = seq(nrow(.)), .before = 1)
    return(df)
}

# サンプルデータ
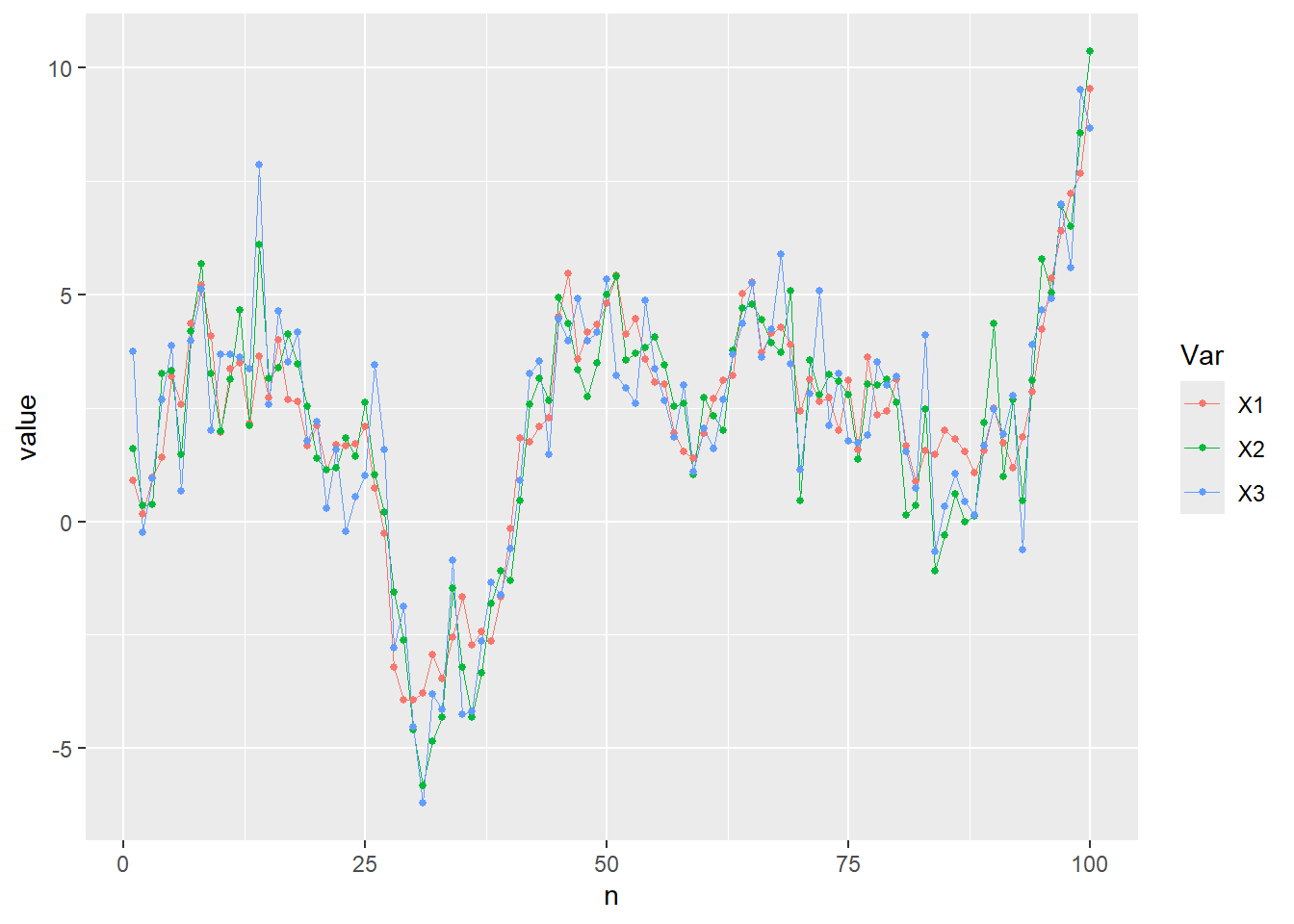
df <- func_sample_vector(p = 0, n = 100)
ggplot(data = gather(data = df, key = "Var", value = "value", colnames(df)[-1]),
    mapping = aes(x = n, y = value, col = Var)) + geom_line(size = 0.1) + geom_point(size = 1)

Figure 1

# サンプルデータの和分次数を確認する。
diff(df$X1) %>%
    adf.test()

    Augmented Dickey-Fuller Test

data:  .
Dickey-Fuller = -3.4718, Lag order = 4, p-value = 0.04823
alternative hypothesis: stationary

# サンプルデータの和分次数を確認する。
diff(df$X2) %>%
    adf.test()

    Augmented Dickey-Fuller Test

data:  .
Dickey-Fuller = -3.775, Lag order = 4, p-value = 0.02297
alternative hypothesis: stationary

# サンプルデータの和分次数を確認する。
diff(df$X3) %>%
    adf.test()

    Augmented Dickey-Fuller Test

data:  .
Dickey-Fuller = -4.0262, Lag order = 4, p-value = 0.01088
alternative hypothesis: stationary

すべてI(1)

# レベル系列のラグ次数指定
K <- max(2, VARselect(df[, -1])$selection["AIC(n)"])
K

[1] 2

ヨハンセン検定

トレース検定

ca.jo(x = df[, -1], type = "trace", ecdet = "trend", K = K, spec = "transitory") %>%
    summary()

###################### 
# Johansen-Procedure # 
###################### 

Test type: trace statistic , with linear trend in cointegration 

Eigenvalues (lambda):
[1] 0.3831285059810191073737 0.3114568088192631867273 0.0265498511346416443679
[4] 0.0000000000000003885781

Values of teststatistic and critical values of test:

          test 10pct  5pct  1pct
r <= 2 |  2.64 10.49 12.25 16.26
r <= 1 | 39.21 22.76 25.32 30.45
r = 0  | 86.55 39.06 42.44 48.45

Eigenvectors, normalised to first column:
(These are the cointegration relations)

                X1.l1        X2.l1       X3.l1  trend.l1
X1.l1     1.000000000  1.000000000  1.00000000 1.0000000
X2.l1     0.299798679 -1.816326770  0.25999585 0.4164079
X3.l1    -1.255409079  0.941888771  0.07418501 0.7879795
trend.l1 -0.003970592 -0.005142918 -0.09979786 0.2206813

Weights W:
(This is the loading matrix)

          X1.l1       X2.l1       X3.l1                 trend.l1
X1.d 0.01304579 -0.06791381 -0.04480053 0.0000000000000003505061
X2.d 0.42320999  0.52544418 -0.04566304 0.0000000000000003241345
X3.d 1.00733093  0.11154762 -0.03673650 0.0000000000000002497965

1. Values of teststatistic and critical values of test:を確認する。
2. 最下段の\(r=0\)を確認すると、検定統計量(test)は5%の臨界値を超えているため\(r=0\)、つまり、帰無仮説「共和分は多くとも\(0\)個である」は棄却される\(\Leftrightarrow\)帰無仮説「正方係数行列\(\Pi\)の固有値の合計(trace)はゼロである」は棄却される。
3. 下から2段目\(r\leq1\)を確認すると、検定統計量(test)は5%の臨界値を超えているため\(r\leq1\)、つまり、帰無仮説「共和分が多くとも\(1\)個である」は棄却される\(\Leftrightarrow\)帰無仮説「正方係数行列\(\Pi\)の固有値のうち最大固有値を除いた固有値の合計(trace)はゼロである」は棄却される。
4. 最上段の\(r\leq2\)を確認すると、検定統計量(test)は5%の臨界値を下回っているため\(r\leq2\)、つまり、帰無仮説「共和分が多くとも\(2\)個である」は棄却されない\(\Leftrightarrow\)帰無仮説「正方係数行列\(\Pi\)の固有値のうち大きい順から2つを除いた固有値の合計(trace)はゼロである」は棄却されない。
5. よって共和分関係は2つ存在する。

固有値検定

ca.jo(x = df[, -1], type = "eigen", ecdet = "trend", K = K, spec = "transitory") %>%
    summary()

###################### 
# Johansen-Procedure # 
###################### 

Test type: maximal eigenvalue statistic (lambda max) , with linear trend in cointegration 

Eigenvalues (lambda):
[1] 0.3831285059810191073737 0.3114568088192631867273 0.0265498511346416443679
[4] 0.0000000000000003885781

Values of teststatistic and critical values of test:

          test 10pct  5pct  1pct
r <= 2 |  2.64 10.49 12.25 16.26
r <= 1 | 36.57 16.85 18.96 23.65
r = 0  | 47.34 23.11 25.54 30.34

Eigenvectors, normalised to first column:
(These are the cointegration relations)

                X1.l1        X2.l1       X3.l1  trend.l1
X1.l1     1.000000000  1.000000000  1.00000000 1.0000000
X2.l1     0.299798679 -1.816326770  0.25999585 0.4164079
X3.l1    -1.255409079  0.941888771  0.07418501 0.7879795
trend.l1 -0.003970592 -0.005142918 -0.09979786 0.2206813

Weights W:
(This is the loading matrix)

          X1.l1       X2.l1       X3.l1                 trend.l1
X1.d 0.01304579 -0.06791381 -0.04480053 0.0000000000000003505061
X2.d 0.42320999  0.52544418 -0.04566304 0.0000000000000003241345
X3.d 1.00733093  0.11154762 -0.03673650 0.0000000000000002497965

1. Values of teststatistic and critical values of test:を確認する。
2. 最下段の\(r=0\)を確認すると、検定統計量(test)は5%の臨界値を超えているため\(r=0\)、つまり、帰無仮説「共和分は多くとも\(0\)個である」は棄却される\(\Leftrightarrow\)帰無仮説「正方係数行列\(\Pi\)の最大固有値はゼロである」は棄却される。
3. 下から2段目\(r\leq1\)を確認すると、検定統計量(test)は5%の臨界値を超えているため\(r\leq1\)、つまり、帰無仮説「共和分が多くとも\(1\)個である」は棄却される\(\Leftrightarrow\)帰無仮説「正方係数行列\(\Pi\)の固有値のうち2番目に大きい固有値はゼロである」は棄却される。
4. 最上段の\(r\leq2\)を確認すると、検定統計量(test)は5%の臨界値を下回っているため\(r\leq2\)、つまり、帰無仮説「共和分が多くとも\(2\)個である」は棄却されない\(\Leftrightarrow\)「正方係数行列\(\Pi\)の固有値のうち3番目に大きい固有値はゼロである」は棄却されない。
5. よって共和分関係は2つ存在する。

エンゲル–グレンジャー検定

X:説明変数、Y:目的変数

egcm(X = df[, 2], Y = df[, 3], debias = T, include.const = T, i1test = "adf", urtest = "adf",
    p.value = 0.05) %>%
    summary()

Y[i] =   1.0478 X[i] -   0.1407 + R[i], R[i] =   0.1528 R[i-1] + eps[i], eps ~ N(0,  0.9901^2)
        (0.0404)        (0.5129)                (0.1000)

R[100] = 0.5080 (t = 0.510)

Unit Root Tests of Residuals
                                                    Statistic    p-value
  Augmented Dickey Fuller (ADF)                        -3.834    0.00990
  Phillips-Perron (PP)                                -84.876    0.00010
  Pantula, Gonzales-Farias and Fuller (PGFF)            0.127    0.00010
  Elliott, Rothenberg and Stock DF-GLS (ERSD)          -2.372    0.07964
  Johansen's Trace Test (JOT)                         -41.657    0.00010
  Schmidt and Phillips Rho (SPR)                      -31.720    0.00904

Variances
  SD(diff(X))          =   1.011589
  SD(diff(Y))          =   1.598928
  SD(diff(residuals))  =   1.319615
  SD(residuals)        =   0.996310
  SD(innovations)      =   0.990148

Half life       =   0.368972
R[last]         =   0.508033 (t=0.51)

残差の単位根検定にADF検定を適用すると\(x_1\)を説明変数、\(x_2\)を目的変数とした線形結合の残差の単位根は棄却される。つまり共和分\(x_1\)と\(x_2\)に共和分関係あり。検定統計量は-3.834。

# 残差の単位根検定であるためtypeはトレンド項なし、ドリフト項なしとする。
lm(formula = df[, 3] ~ df[, 2])$resi %>%
    urca::ur.df(type = "none", lags = trunc((nrow(df) - 1)^(1/3))) %>%
    summary()

############################################### 
# Augmented Dickey-Fuller Test Unit Root Test # 
############################################### 

Test regression none 


Call:
lm(formula = z.diff ~ z.lag.1 - 1 + z.diff.lag)

Residuals:
     Min       1Q   Median       3Q      Max 
-2.72077 -0.63920 -0.06777  0.67820  2.57977 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
z.lag.1     -0.80609    0.21024  -3.834 0.000233 ***
z.diff.lag1 -0.04700    0.18819  -0.250 0.803369    
z.diff.lag2 -0.09239    0.16522  -0.559 0.577419    
z.diff.lag3 -0.08234    0.13603  -0.605 0.546499    
z.diff.lag4 -0.10196    0.10335  -0.987 0.326510    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.003 on 90 degrees of freedom
Multiple R-squared:  0.4363,    Adjusted R-squared:  0.405 
F-statistic: 13.93 on 5 and 90 DF,  p-value: 0.000000000445


Value of test-statistic is: -3.8341 

Critical values for test statistics: 
     1pct  5pct 10pct
tau1 -2.6 -1.95 -1.61

こちらも検定統計量は-3.834と一致します。

参考引用資料

• 村尾博(2019),『Rで学ぶVAR実証分析』,オーム社,pp.166-174
• https://www.r-econometrics.com/timeseries/vecintro/
• http://user.keio.ac.jp/~nagakura/R/R_cointegration.pdf

---

ヨハンセン検定

ヨハンセン検定では次の回帰モデル(ベクトル誤差修正モデル)を用いる。\[\Delta y_t=\Pi y_{t-1}+\displaystyle\sum_{i=1}^{p-1}\Gamma_i\Delta y_{t-i}+B_zz_t+u_t\]ここで\(\Pi\)は\((K,K)\)の正方係数行列。

正方行列であるため\[\Pi=P^{-1}AP\]と対角化したとき対角行列\(A\)の対角要素(固有値)のうちゼロでない固有値の数が\(\Pi\)の階数となる。

\(K\)は検定対称の要素数であり内生変数(従属変数、非説明変数。対して外生変数は独立変数、説明変数)の個数である必要はない。内生変数の個数が4個であり、そのうち3個が検定対象である場合\(K=3\)

係数行列\(\Pi\)のランクについて

1. \(\mathrm{rank}(\Pi)=K\)の場合(フルランクの場合)
   • ベクトル\(y_t\)の\(K\)個の内生変数に対して\(K\)個の共和分ベクトルが存在することを意味する。
   • \(K\)個の内生変数がすべて\(I(1)\)(1次の和分過程)であれば最大で\(K-1\)個の共和分ベクトルが存在する。
   • \(\Pi\)がフルランクの場合、\(K\)個の内生変数はすべて\(I(0)\)。よって採用するモデルはレベルVARとなる。
2. \(\mathrm{rank}(\Pi)=r,(0<r<K)\)の場合
   • ベクトル\(y_t\)の\(K\)個の内生変数に対して\(0<r<K\)で示す\(r\)個の共和分ベクトル(共和分ランク)が存在しベクトル誤差修正モデル(VEC)を構築するケースとなる。
   • ベクトル\(y_t\)に\(I(0)\)の内生変数が1個含まれていれば共和分ランクは1つ増え、2個含まれていれば共和分ランクは2増える。よって\(y_t\)に\(I(0)\)の内生変数が含まれている場合、共和分ランク\(r\)から\(I(0)\)の内生変数の個数を引いた数が\(I(1)\)間の本来の共和分ランクとなる。
3. \(\mathrm{rank}(\Pi)=0\)の場合(ゼロランクの場合)
   • ベクトル\(y_t\)に含まれる\(K\)個の内生変数に対し共和分ベクトルは存在しない。
   • \(\mathrm{rank}(\Pi)=0\)の場合、\(K\)個の内生変数はすべて\(I(1)\)(1次の和分過程)であり、かつ\(I(1)\)の内生変数間に共和分が存在しないことを意味する。

ヨハンセン検定にはトレース検定と最大固有値検定あり。

トレース検定

1. \(\mathrm{H}_0:r_0\)個の共和分ベクトルが存在する。
2. \(\mathrm{H}_1:K\)個の共和分ベクトルが存在する。

• \(K\)個の共和分ベクトルが存在とは\(y_t\)に含まれる\(K\)個の内生変数が全て定常過程\(I(0)\)であることを意味する。
• トレース検定統計量は\[\mathrm{LR}_{\mathrm{trace}}(r_0)=-2\{\mathrm{logL}(r_0)-\mathrm{LogL}(K)\}=-T\displaystyle\sum_{i=r+1}^K\mathrm{log}(1-\hat{\lambda}_i)\]ここで\(\mathrm{logL}()\)は対数尤度関数、\(\hat{\lambda}\)は行列\(\Pi\)の固有値。
• 共和分ランクが\(r\)のとき残り\(K-r\)個の固有値\(\lambda_i(i=r+1,\cdots,K)\)はゼロとなる性質を利用するのが検定統計量\(\mathrm{LR_{trace}}(r_0)\)であり、残り\(K-r_0\)個の推定固有値\(\hat{\lambda}_i(i=r_0+1,\cdots,K)\)を調べる。
• \(\mathrm{H_0}\)が真であれば\(\hat{\lambda}_i(i=r_0+1,\cdots,K)\)がゼロとなり\(\mathrm{LR_{trace}}(r_0)\)もゼロとなる。
• なおこの検定はゼロを基点とする右片側検定である。

最大固有値検定

1. \(\mathrm{H}_0:r_0\)個の共和分ベクトルが存在する。
2. \(\mathrm{H}_1:r_0+1\)個の共和分ベクトルが存在する。

• \(\mathrm{H}_0\)は検定対象の\(y_t\)には高々\(r_0\)組の共和分関係がある、という意味であり最大固有値検定統計量は\[\mathrm{LR_{max}}(r_0)=-T\mathrm{log}(1-\hat{\lambda}_{r_0+1})\]
• \(\mathrm{H_0}\)が真であれば\(\hat{\lambda}_{r_0+1}\)がゼロとなり\(\mathrm{LR_{max}}(r_0)\)もゼロとなる。
• なおこの検定もトレース検定同様、ゼロを基点とする右片側検定である。

検定アルゴリズム(トレース検定、最大固有値検定)は以下の通り。

1. \(\mathrm{H}_0\)の\(r\)を\(r=1,r=1,r=2,\cdots,r=K-1,r=K\)と変化させ、例えば\(r=0\)が棄却されなければ共和分ランクは\(r=0\)となり共和分関係なし。
2. \(r=0\)が棄却され\(r=1\)が棄却されないとき共和分ランクは\(r=1\)となり1個の共和分ベクトルが存在する。

ヨハンセン検定の場合\(I(1)\)(1次の和分過程)のみの組み合わせが共和分検定の対象になるが\(I(0)\)が混在してもよい。その際、変数ベクトル\(y_t\)における\(I(0)\)過程の存在は共和分ランクの増加として現れる。

エンゲル–グレンジャー検定

検定の理屈は次の通り

1. ある\(I(1)\)過程(\(y_1\))を別の\(I(1)\)過程(\((y_2)\))に線形回帰させ残差を得る。
2. その残差に単位根検定を行い\(I(0)\)過程であれば\(y_1,y_2\)は共和分関係にある。

検定の手順は次の通り(例として変数が2個の場合)

1. 2個の\(I(1)\)過程のみを対象とし\[y_1\sim I(1),\,y_2\sim I(1)\]とする。
2. 回帰式\[y_{1t}=\beta_1+\beta_2 y_{2t}+u_t\]の推定から残差\(\{\hat{u}_t\}\)を得る。
3. 2つの均衡する系列からの回帰残差であれば\(\{\hat{u}_t\}\)は定常であり共和分関係。
4. 単位根をもっているならば2系列は共和分関係にない。
5. 残差\(\{\hat{u}_t\}\)に対して次のDF検定(上段)またはADF検定(下段)を行う。ここで\(\epsilon_t\)はホワイトノイズ。
   • AR(1)の場合: \(\Delta\hat{u}_t=(\rho-1)\hat{u}_t+\epsilon_t\)
   • AR(p)の場合: \(\Delta\hat{u}_t=(\rho-1)\hat{u}_t+ \displaystyle\sum_{i=1}^{p-1}\Delta\hat{u}_{t-1}+\epsilon_t\)
   • 検定対象は残差であるためドリフト項およびトレンド項なしのnoneモデルで検定する。
     • \(H_0:\rho-1=0\quad\)(単位根あり)
     • \(H_1:\rho-1<0\quad\)(単位根なし)
   • 帰無仮説が棄却された場合、残差に単位根なし。つまり2系列は共和分関係にあり。
   • 検定対象の残差は推定量であることから帰無分布にディッキー=フラー分布は使えない。

参考引用資料

• 村尾博(2019),『Rで学ぶVAR実証分析』,オーム社,pp.23-24,154-158

最終更新

Sys.time()

[1] "2025-01-03 13:33:12 JST"

R、Quarto、Package

R.Version()$version.string

[1] "R version 4.4.2 Patched (2024-12-13 r87441 ucrt)"

quarto::quarto_version()

[1] '1.6.39'

packageVersion(pkg = 'tidyverse')

[1] '2.0.0'

著者

• アセット･マネジメント･コンサルティング株式会社 https://www.am-consulting.co.jp
• 法人概要 https://www.contact.am-consulting.co.jp/company-brochure/
• 代表取締役 三竹道雄 https://www.contact.am-consulting.co.jp/mitake-michio/
• 公開コンテンツリスト https://www.am-consulting.co.jp/amc-all-contents
• Charts https://www.am-consulting.co.jp/charts
• 法令検索 https://www.laws.am-consulting.co.jp/
• SaECaNet https://www.saecanet.com/
• twitter https://twitter.com/amc_corporation
• youtube https://www.youtube.com/user/michiomitake
• twilog https://twilog.togetter.com/amc_corporation
• github https://github.com/am-consulting