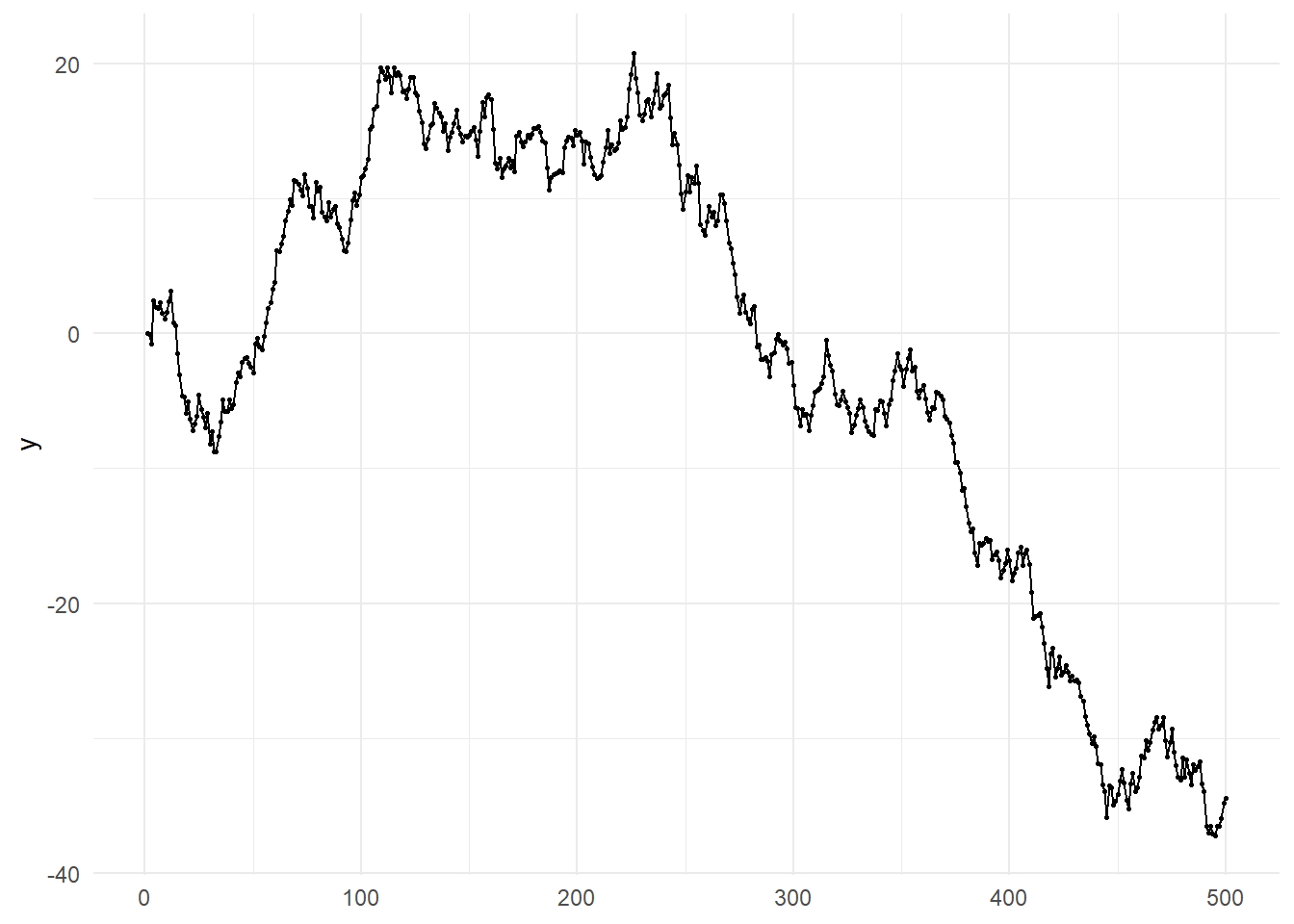Rで時系列分析:単位根検定:検定統計量

Rでデータサイエンス

単位根検定:検定統計量

# サンプル時系列データ
library(ggplot2)
library(dplyr)
library(urca)
library(tibble)
samplesize <- 500
y <- rnorm(n = samplesize) %>%
    cumsum()
ggplot(mapping = aes(x = seq(y), y = y)) + geom_line(size = 0.5) + geom_point(size = 0.5) + theme_minimal() + theme(axis.title.x = element_blank())

# 検定統計量を算出する関数
func_test_statistic_of_adf <- function(y, p, drift = T, trend = T, without_ylag1_term = F) {
    # 原系列をデータフレーム化
    df0 <- y %>%
        data.frame()
    colnames(df0) <- "y_t"
    tail(df0)
    # トレンド項追加
    df1 <- df0 %>%
        add_column(t = seq(nrow(df0)), .before = 1)
    tail(df1)
    # (ラグ = 1)項追加
    df1$`y_{t-1}` <- head(df1$y_t, -1) %>%
        c(NA, .)
    tail(df1)
    # 系列相関の影響を除去するための項を追加
    ## 1階差分系列の作成
    diff <- df1$y_t %>%
        diff(lag = 1, differences = 1)
    head(diff)
    ## (p + 1)次までのラグをとる
    lagdf0 <- embed(diff, p + 1)
    head(lagdf0)
    ## df1と列数をあわせる
    lagdf <- lagdf0 %>%
        rbind(matrix(nrow = p + 1, ncol = p + 1), .)
    head(lagdf, p + 1 + 6)
    df2 <- cbind(df1, lagdf)
    head(df2, p + 1 + 6)
    # 差分系列の列名設定。4列目は目的変数となる Δy_t
    colnames(df2)[4:(4 + p)] <- {
        if (0 < p) {
            c(0, seq(p))
        } else {
            0
        }
    } %>%
        paste0("Δy_{t-", ., "}")
    tail(df2)
    colnames(df2) <- colnames(df2) %>%
        gsub("\\{t-0\\}", "t", .)
    tail(df2)
    # NA行削除
    df <- df2 %>%
        na.omit()
    head(df)
    # 説明変数とする列を設定
    col_explanatory_variable <- if (0 < p) {
        5:ncol(df)
    } else {
        NULL
    }
    if (!without_ylag1_term)
        col_explanatory_variable <- c(3, col_explanatory_variable)
    if (trend)
        col_explanatory_variable <- c(1, col_explanatory_variable)
    col_explanatory_variable
    # 線形回帰
    var_obj <- df[, 4, drop = F] %>%
        colnames()
    var_exp <- df[, col_explanatory_variable, drop = F] %>%
        colnames() %>%
        paste0("`", ., "`", collapse = " + ")
    adf_model <- paste0("`", var_obj, "` ~ ", var_exp, ifelse(drift, " + 1", " + 0")) %>%
        gsub("``", "", .) %>%
        eval()
    result_lm <- lm(formula = adf_model, df) %>%
        summary()
    adf_model <- adf_model %>%
        gsub("`", "", .)
    return(list(df = tail(df), result_lm = result_lm, adf_model = adf_model))
}

\(\tau\)検定統計量(\(\tau_3,\tau_2,\tau_1\))

\(\tau_3\)

モデル:trend
検定統計量:\(\tau_3\)
仮説\(\,\,\,\textrm{H}_0:\rho - 1=0\)
ドリフト項あり、トレンド項あり

\[\Delta y_t=\beta_1+\beta_2t+(\rho-1) y_{t-1}+\displaystyle \sum_{i=1}^{p-1}\gamma_i \Delta y_{t-i} + u_t\]

p <- 3
drift <- T
trend <- T
without_ylag1_term <- F
result <- func_test_statistic_of_adf(y = y, p = p, drift = drift, trend = trend, without_ylag1_term = without_ylag1_term)
result

$df
      t       y_t   y_{t-1}      Δy_t  Δy_{t-1}  Δy_{t-2}  Δy_{t-3}
495 495 -37.22485 -37.05784 -0.1670074 -0.5856425  0.5415540 -0.5249681
496 496 -36.52155 -37.22485  0.7032977 -0.1670074 -0.5856425  0.5415540
497 497 -36.49747 -36.52155  0.0240795  0.7032977 -0.1670074 -0.5856425
498 498 -35.90126 -36.49747  0.5962114  0.0240795  0.7032977 -0.1670074
499 499 -34.80263 -35.90126  1.0986273  0.5962114  0.0240795  0.7032977
500 500 -34.46493 -34.80263  0.3377050  1.0986273  0.5962114  0.0240795

$result_lm

Call:
lm(formula = adf_model, data = df)

Residuals:
     Min       1Q   Median       3Q      Max 
-2.91002 -0.73624  0.01996  0.70541  2.81531 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)  
(Intercept)  0.2074432  0.1244892   1.666   0.0963 .
t           -0.0011518  0.0004825  -2.387   0.0174 *
`y_{t-1}`   -0.0057019  0.0041906  -1.361   0.1743  
`Δy_{t-1}`  0.0610040  0.0446326   1.367   0.1723  
`Δy_{t-2}`  0.0112309  0.0447548   0.251   0.8020  
`Δy_{t-3}` -0.0418894  0.0447289  -0.937   0.3495  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.022 on 490 degrees of freedom
Multiple R-squared:  0.01849,   Adjusted R-squared:  0.008478 
F-statistic: 1.847 on 5 and 490 DF,  p-value: 0.1023


$adf_model
[1] "Δy_t ~ t + y_{t-1} + Δy_{t-1} + Δy_{t-2} + Δy_{t-3} + 1"

# y_{t-1}の係数のt値
result$result_lm %>%
    {
        .$coef[3, 3, drop = F]
    }

            t value
`y_{t-1}` -1.360641

# Rのur.df {urca}の結果と照合します。
ur.df(y = y, type = "trend", lags = p) %>%
    summary() %>%
    .@teststat
# tau3の結果は一致します。

               tau3     phi2     phi3
statistic -1.360641 2.804248 3.024995

\(\tau_2\)

モデル:drift
検定統計量:\(\tau_2\)
仮説\(\,\,\,\textrm{H}_0:\rho - 1=0\)
ドリフト項あり、トレンド項なし

\[\Delta y_t=\beta_1+(\rho-1) y_{t-1}+\displaystyle \sum_{i=1}^{p-1}\gamma_i \Delta y_{t-i} + u_t\]

p <- 0
drift <- T
trend <- F
without_ylag1_term <- F
result <- func_test_statistic_of_adf(y = y, p = p, drift = drift, trend = trend, without_ylag1_term = without_ylag1_term)
result

$df
      t       y_t   y_{t-1}      Δy_t
495 495 -37.22485 -37.05784 -0.1670074
496 496 -36.52155 -37.22485  0.7032977
497 497 -36.49747 -36.52155  0.0240795
498 498 -35.90126 -36.49747  0.5962114
499 499 -34.80263 -35.90126  1.0986273
500 500 -34.46493 -34.80263  0.3377050

$result_lm

Call:
lm(formula = adf_model, data = df)

Residuals:
    Min      1Q  Median      3Q     Max 
-2.9816 -0.7229  0.0099  0.6819  3.3040 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.065383   0.046621  -1.402    0.161
`y_{t-1}`    0.001947   0.002824   0.690    0.491

Residual standard error: 1.035 on 497 degrees of freedom
Multiple R-squared:  0.000956,  Adjusted R-squared:  -0.001054 
F-statistic: 0.4756 on 1 and 497 DF,  p-value: 0.4907


$adf_model
[1] "Δy_t ~ y_{t-1} + 1"

# y_{t-1}の係数のt値
result$result_lm %>%
    {
        .$coef[2, 3, drop = F]
    }

            t value
`y_{t-1}` 0.6896312

# Rのur.df {urca}の結果と照合します。
ur.df(y = y, type = "drift", lags = p) %>%
    summary() %>%
    .@teststat
# tau2の結果は一致します。

               tau2     phi1
statistic 0.6896312 1.349341

\(tau_1\)

モデル:none
検定統計量:\(\tau_1\)
仮説\(\,\,\,\textrm{H}_0:\rho - 1=0\)
ドリフト項なし、トレンド項なし

\[\Delta y_t=(\rho-1) y_{t-1}+ \sum_{i=1}^{p-1}\gamma_i \Delta y_{t-i} + u_t\]

p <- 6
drift <- F
trend <- F
without_ylag1_term <- F
result <- func_test_statistic_of_adf(y = y, p = p, drift = drift, trend = trend, without_ylag1_term = without_ylag1_term)
result

$df
      t       y_t   y_{t-1}      Δy_t  Δy_{t-1}  Δy_{t-2}  Δy_{t-3}
495 495 -37.22485 -37.05784 -0.1670074 -0.5856425  0.5415540 -0.5249681
496 496 -36.52155 -37.22485  0.7032977 -0.1670074 -0.5856425  0.5415540
497 497 -36.49747 -36.52155  0.0240795  0.7032977 -0.1670074 -0.5856425
498 498 -35.90126 -36.49747  0.5962114  0.0240795  0.7032977 -0.1670074
499 499 -34.80263 -35.90126  1.0986273  0.5962114  0.0240795  0.7032977
500 500 -34.46493 -34.80263  0.3377050  1.0986273  0.5962114  0.0240795
     Δy_{t-4}  Δy_{t-5}  Δy_{t-6}
495 -2.5709663 -0.5797270 -1.5836468
496 -0.5249681 -2.5709663 -0.5797270
497  0.5415540 -0.5249681 -2.5709663
498 -0.5856425  0.5415540 -0.5249681
499 -0.1670074 -0.5856425  0.5415540
500  0.7032977 -0.1670074 -0.5856425

$result_lm

Call:
lm(formula = adf_model, data = df)

Residuals:
     Min       1Q   Median       3Q      Max 
-2.92681 -0.74861 -0.00368  0.66514  2.61225 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)  
`y_{t-1}`    0.0009277  0.0028805   0.322   0.7475  
`Δy_{t-1}`  0.0707226  0.0454728   1.555   0.1205  
`Δy_{t-2}`  0.0240812  0.0454234   0.530   0.5962  
`Δy_{t-3}` -0.0384392  0.0454349  -0.846   0.3980  
`Δy_{t-4}`  0.0144336  0.0449413   0.321   0.7482  
`Δy_{t-5}`  0.1090063  0.0449507   2.425   0.0157 *
`Δy_{t-6}`  0.0316693  0.0451640   0.701   0.4835  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.026 on 486 degrees of freedom
Multiple R-squared:  0.02247,   Adjusted R-squared:  0.008391 
F-statistic: 1.596 on 7 and 486 DF,  p-value: 0.1342


$adf_model
[1] "Δy_t ~ y_{t-1} + Δy_{t-1} + Δy_{t-2} + Δy_{t-3} + Δy_{t-4} + Δy_{t-5} + Δy_{t-6} + 0"

# y_{t-1}の係数のt値
result$result_lm %>%
    {
        .$coef[1, 3, drop = F]
    }

            t value
`y_{t-1}` 0.3220682

# Rのur.df {urca}の結果と照合します。
ur.df(y = y, type = "none", lags = p) %>%
    summary() %>%
    .@teststat
# tau1の結果は一致します。

               tau1
statistic 0.3220682

\(\phi\)検定統計量(\(phi_3,\phi_2,\phi_1\))

複数係数の仮説検定となりますのでF検定を利用
分散比は以下の通り\[\frac{\left[\textrm{SSR(restricted)}-\textrm{SSR(restricted)}\right]/r}{\textrm{SSR(restricted)}/(T-k)}\]ここで\(r\):帰無仮説の制約条件数,\(T\):サンプルサイズ,\(k\):制約無しの場合のパラメータ数,\(\rho\):ラグ次数

\(\phi_3\)

モデル:trend
検定統計量:\(\phi_3\)
仮説\(\,\,\,\textrm{H}_0:\rho - 1=\beta_2=0\)

\[\Delta y_t=\beta_1+\beta_2t+(\rho-1) y_{t-1}+\displaystyle\sum_{i=1}^{p-1}\gamma_i\Delta y_{t-i} + u_t\]

# ラグ次数を7とする。
p <- 7
drift <- T

# 帰無仮説の制約条件なし
trend <- T
without_ylag1_term <- F
unrestricted <- func_test_statistic_of_adf(y = y, p = p, drift = drift, trend = trend, without_ylag1_term = without_ylag1_term)
unrest_resi <- unrestricted$result_lm$residuals
ssr_unrestricted <- sum(unrest_resi^2)
unrestricted

$df
      t       y_t   y_{t-1}      Δy_t  Δy_{t-1}  Δy_{t-2}  Δy_{t-3}
495 495 -37.22485 -37.05784 -0.1670074 -0.5856425  0.5415540 -0.5249681
496 496 -36.52155 -37.22485  0.7032977 -0.1670074 -0.5856425  0.5415540
497 497 -36.49747 -36.52155  0.0240795  0.7032977 -0.1670074 -0.5856425
498 498 -35.90126 -36.49747  0.5962114  0.0240795  0.7032977 -0.1670074
499 499 -34.80263 -35.90126  1.0986273  0.5962114  0.0240795  0.7032977
500 500 -34.46493 -34.80263  0.3377050  1.0986273  0.5962114  0.0240795
     Δy_{t-4}  Δy_{t-5}  Δy_{t-6}  Δy_{t-7}
495 -2.5709663 -0.5797270 -1.5836468  0.3588198
496 -0.5249681 -2.5709663 -0.5797270 -1.5836468
497  0.5415540 -0.5249681 -2.5709663 -0.5797270
498 -0.5856425  0.5415540 -0.5249681 -2.5709663
499 -0.1670074 -0.5856425  0.5415540 -0.5249681
500  0.7032977 -0.1670074 -0.5856425  0.5415540

$result_lm

Call:
lm(formula = adf_model, data = df)

Residuals:
     Min       1Q   Median       3Q      Max 
-2.77476 -0.71547 -0.00771  0.70375  2.75985 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)  
(Intercept)  0.2262141  0.1275450   1.774   0.0768 .
t           -0.0011928  0.0004932  -2.418   0.0160 *
`y_{t-1}`   -0.0064336  0.0042410  -1.517   0.1299  
`Δy_{t-1}`  0.0663512  0.0453096   1.464   0.1437  
`Δy_{t-2}`  0.0237064  0.0454616   0.521   0.6023  
`Δy_{t-3}` -0.0465346  0.0452755  -1.028   0.3046  
`Δy_{t-4}`  0.0092247  0.0452989   0.204   0.8387  
`Δy_{t-5}`  0.1000152  0.0448250   2.231   0.0261 *
`Δy_{t-6}`  0.0277705  0.0450219   0.617   0.5376  
`Δy_{t-7}` -0.0697938  0.0449936  -1.551   0.1215  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.02 on 482 degrees of freedom
Multiple R-squared:  0.03666,   Adjusted R-squared:  0.01867 
F-statistic: 2.038 on 9 and 482 DF,  p-value: 0.03368


$adf_model
[1] "Δy_t ~ t + y_{t-1} + Δy_{t-1} + Δy_{t-2} + Δy_{t-3} + Δy_{t-4} + Δy_{t-5} + Δy_{t-6} + Δy_{t-7} + 1"

# 帰無仮説の制約条件あり
trend <- F
without_ylag1_term <- T
restricted <- func_test_statistic_of_adf(y = y, p = p, drift = drift, trend = trend, without_ylag1_term = without_ylag1_term)
rest_resi <- restricted$result_lm$residuals
ssr_restricted <- sum(rest_resi^2)
restricted

$df
      t       y_t   y_{t-1}      Δy_t  Δy_{t-1}  Δy_{t-2}  Δy_{t-3}
495 495 -37.22485 -37.05784 -0.1670074 -0.5856425  0.5415540 -0.5249681
496 496 -36.52155 -37.22485  0.7032977 -0.1670074 -0.5856425  0.5415540
497 497 -36.49747 -36.52155  0.0240795  0.7032977 -0.1670074 -0.5856425
498 498 -35.90126 -36.49747  0.5962114  0.0240795  0.7032977 -0.1670074
499 499 -34.80263 -35.90126  1.0986273  0.5962114  0.0240795  0.7032977
500 500 -34.46493 -34.80263  0.3377050  1.0986273  0.5962114  0.0240795
     Δy_{t-4}  Δy_{t-5}  Δy_{t-6}  Δy_{t-7}
495 -2.5709663 -0.5797270 -1.5836468  0.3588198
496 -0.5249681 -2.5709663 -0.5797270 -1.5836468
497  0.5415540 -0.5249681 -2.5709663 -0.5797270
498 -0.5856425  0.5415540 -0.5249681 -2.5709663
499 -0.1670074 -0.5856425  0.5415540 -0.5249681
500  0.7032977 -0.1670074 -0.5856425  0.5415540

$result_lm

Call:
lm(formula = adf_model, data = df)

Residuals:
     Min       1Q   Median       3Q      Max 
-2.81006 -0.71492  0.00235  0.72476  2.67218 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)  
(Intercept) -0.06194    0.04689  -1.321    0.187  
`Δy_{t-1}`  0.07147    0.04534   1.576    0.116  
`Δy_{t-2}`  0.02876    0.04547   0.633    0.527  
`Δy_{t-3}` -0.04107    0.04522  -0.908    0.364  
`Δy_{t-4}`  0.01488    0.04524   0.329    0.742  
`Δy_{t-5}`  0.10711    0.04473   2.394    0.017 *
`Δy_{t-6}`  0.03334    0.04496   0.742    0.459  
`Δy_{t-7}` -0.06443    0.04492  -1.434    0.152  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.024 on 484 degrees of freedom
Multiple R-squared:  0.02469,   Adjusted R-squared:  0.01058 
F-statistic:  1.75 on 7 and 484 DF,  p-value: 0.09536


$adf_model
[1] "Δy_t ~ Δy_{t-1} + Δy_{t-2} + Δy_{t-3} + Δy_{t-4} + Δy_{t-5} + Δy_{t-6} + Δy_{t-7} + 1"

# 分散比
r <- 2
k <- 3 + p
Fvalue <- ((ssr_restricted - ssr_unrestricted)/r)/(ssr_unrestricted/(length(unrest_resi) - k))
Fvalue

[1] 2.99439

# Rのur.df {urca}の結果と照合します。
ur.df(y = y, type = "trend", lags = p) %>%
    summary() %>%
    .@teststat
# phi3の結果は一致します。

               tau3     phi2    phi3
statistic -1.517009 2.582697 2.99439

\(\phi_2\)

モデル:trend
検定統計量:\(\phi_2\)
仮説\(\,\,\,\textrm{H}_0:\rho -1=\beta_1= \beta_2=0\)

\[\Delta y_t=\beta_1+\beta_2t+(\rho-1) y_{t-1}+\displaystyle\sum_{i=1}^{p-1}\gamma_i \Delta y_{t-i} + u_t\]

# ラグ次数を5とする。
p <- 5

# 帰無仮説の制約条件なし
drift <- T
trend <- T
without_ylag1_term <- F
unrestricted <- func_test_statistic_of_adf(y = y, p = p, drift = drift, trend = trend, without_ylag1_term = without_ylag1_term)
unrest_resi <- unrestricted$result_lm$residuals
ssr_unrestricted <- sum(unrest_resi^2)
unrestricted

$df
      t       y_t   y_{t-1}      Δy_t  Δy_{t-1}  Δy_{t-2}  Δy_{t-3}
495 495 -37.22485 -37.05784 -0.1670074 -0.5856425  0.5415540 -0.5249681
496 496 -36.52155 -37.22485  0.7032977 -0.1670074 -0.5856425  0.5415540
497 497 -36.49747 -36.52155  0.0240795  0.7032977 -0.1670074 -0.5856425
498 498 -35.90126 -36.49747  0.5962114  0.0240795  0.7032977 -0.1670074
499 499 -34.80263 -35.90126  1.0986273  0.5962114  0.0240795  0.7032977
500 500 -34.46493 -34.80263  0.3377050  1.0986273  0.5962114  0.0240795
     Δy_{t-4}  Δy_{t-5}
495 -2.5709663 -0.5797270
496 -0.5249681 -2.5709663
497  0.5415540 -0.5249681
498 -0.5856425  0.5415540
499 -0.1670074 -0.5856425
500  0.7032977 -0.1670074

$result_lm

Call:
lm(formula = adf_model, data = df)

Residuals:
     Min       1Q   Median       3Q      Max 
-2.79844 -0.73152  0.01413  0.72507  2.69572 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)  
(Intercept)  0.2168157  0.1258618   1.723   0.0856 .
t           -0.0011502  0.0004874  -2.360   0.0187 *
`y_{t-1}`   -0.0064541  0.0042088  -1.533   0.1258  
`Δy_{t-1}`  0.0660892  0.0450525   1.467   0.1430  
`Δy_{t-2}`  0.0164903  0.0452083   0.365   0.7154  
`Δy_{t-3}` -0.0436533  0.0447214  -0.976   0.3295  
`Δy_{t-4}`  0.0058659  0.0447304   0.131   0.8957  
`Δy_{t-5}`  0.1021658  0.0447243   2.284   0.0228 *
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.019 on 486 degrees of freedom
Multiple R-squared:  0.03045,   Adjusted R-squared:  0.01649 
F-statistic: 2.181 on 7 and 486 DF,  p-value: 0.03465


$adf_model
[1] "Δy_t ~ t + y_{t-1} + Δy_{t-1} + Δy_{t-2} + Δy_{t-3} + Δy_{t-4} + Δy_{t-5} + 1"

# 帰無仮説の制約条件あり
drift <- F
trend <- F
without_ylag1_term <- T
restricted <- func_test_statistic_of_adf(y = y, p = p, drift = drift, trend = trend, without_ylag1_term = without_ylag1_term)
rest_resi <- restricted$result_lm$residuals
ssr_restricted <- sum(rest_resi^2)
restricted

$df
      t       y_t   y_{t-1}      Δy_t  Δy_{t-1}  Δy_{t-2}  Δy_{t-3}
495 495 -37.22485 -37.05784 -0.1670074 -0.5856425  0.5415540 -0.5249681
496 496 -36.52155 -37.22485  0.7032977 -0.1670074 -0.5856425  0.5415540
497 497 -36.49747 -36.52155  0.0240795  0.7032977 -0.1670074 -0.5856425
498 498 -35.90126 -36.49747  0.5962114  0.0240795  0.7032977 -0.1670074
499 499 -34.80263 -35.90126  1.0986273  0.5962114  0.0240795  0.7032977
500 500 -34.46493 -34.80263  0.3377050  1.0986273  0.5962114  0.0240795
     Δy_{t-4}  Δy_{t-5}
495 -2.5709663 -0.5797270
496 -0.5249681 -2.5709663
497  0.5415540 -0.5249681
498 -0.5856425  0.5415540
499 -0.1670074 -0.5856425
500  0.7032977 -0.1670074

$result_lm

Call:
lm(formula = adf_model, data = df)

Residuals:
     Min       1Q   Median       3Q      Max 
-2.90825 -0.77330 -0.02666  0.64682  2.60070 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)  
`Δy_{t-1}`  0.07562    0.04493   1.683   0.0930 .
`Δy_{t-2}`  0.02516    0.04508   0.558   0.5771  
`Δy_{t-3}` -0.03430    0.04460  -0.769   0.4422  
`Δy_{t-4}`  0.01569    0.04458   0.352   0.7251  
`Δy_{t-5}`  0.11258    0.04451   2.529   0.0117 *
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.024 on 489 degrees of freedom
Multiple R-squared:  0.02084,   Adjusted R-squared:  0.01083 
F-statistic: 2.081 on 5 and 489 DF,  p-value: 0.06644


$adf_model
[1] "Δy_t ~ Δy_{t-1} + Δy_{t-2} + Δy_{t-3} + Δy_{t-4} + Δy_{t-5} + 0"

# 分散比
r <- 3  # phi3との違いは制約条件数です。
k <- 3 + p
Fvalue <- ((ssr_restricted - ssr_unrestricted)/r)/(ssr_unrestricted/(length(unrest_resi) - k))
Fvalue

[1] 2.446296

# Rのur.df {urca}の結果と照合します。
ur.df(y = y, type = "trend", lags = p) %>%
    summary() %>%
    .@teststat
# phi2の結果は一致します。

               tau3     phi2     phi3
statistic -1.533478 2.446296 2.827418

\(\phi_1\)

モデル:drift
検定統計量:\(\phi_1\)
仮説\(\,\,\,\textrm{H}_0:\rho -1=\beta_1=0\)

\[\Delta y_t=\beta_1+(\rho-1) y_{t-1}+\displaystyle\sum_{i=1}^{p-1}\gamma_i \Delta y_{t-i} + u_t\]

# ラグ次数を4とする。
p <- 4
trend <- F

# 帰無仮説の制約条件なし
drift <- T
without_ylag1_term <- F
unrestricted <- func_test_statistic_of_adf(y = y, p = p, drift = drift, trend = trend, without_ylag1_term = without_ylag1_term)
unrest_resi <- unrestricted$result_lm$residuals
ssr_unrestricted <- sum(unrest_resi^2)
unrestricted

$df
      t       y_t   y_{t-1}      Δy_t  Δy_{t-1}  Δy_{t-2}  Δy_{t-3}
495 495 -37.22485 -37.05784 -0.1670074 -0.5856425  0.5415540 -0.5249681
496 496 -36.52155 -37.22485  0.7032977 -0.1670074 -0.5856425  0.5415540
497 497 -36.49747 -36.52155  0.0240795  0.7032977 -0.1670074 -0.5856425
498 498 -35.90126 -36.49747  0.5962114  0.0240795  0.7032977 -0.1670074
499 499 -34.80263 -35.90126  1.0986273  0.5962114  0.0240795  0.7032977
500 500 -34.46493 -34.80263  0.3377050  1.0986273  0.5962114  0.0240795
     Δy_{t-4}
495 -2.5709663
496 -0.5249681
497  0.5415540
498 -0.5856425
499 -0.1670074
500  0.7032977

$result_lm

Call:
lm(formula = adf_model, data = df)

Residuals:
     Min       1Q   Median       3Q      Max 
-2.97330 -0.75020  0.03382  0.71386  2.73905 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.065731   0.046824  -1.404    0.161
`y_{t-1}`    0.001573   0.002863   0.549    0.583
`Δy_{t-1}`  0.071580   0.045373   1.578    0.115
`Δy_{t-2}`  0.014571   0.045023   0.324    0.746
`Δy_{t-3}` -0.038074   0.045026  -0.846    0.398
`Δy_{t-4}`  0.016409   0.044999   0.365    0.716

Residual standard error: 1.028 on 489 degrees of freedom
Multiple R-squared:  0.007843,  Adjusted R-squared:  -0.002301 
F-statistic: 0.7731 on 5 and 489 DF,  p-value: 0.5694


$adf_model
[1] "Δy_t ~ y_{t-1} + Δy_{t-1} + Δy_{t-2} + Δy_{t-3} + Δy_{t-4} + 1"

# 帰無仮説の制約条件あり
drift <- F
without_ylag1_term <- T
restricted <- func_test_statistic_of_adf(y = y, p = p, drift = drift, trend = trend, without_ylag1_term = without_ylag1_term)
rest_resi <- restricted$result_lm$residuals
ssr_restricted <- sum(rest_resi^2)
restricted

$df
      t       y_t   y_{t-1}      Δy_t  Δy_{t-1}  Δy_{t-2}  Δy_{t-3}
495 495 -37.22485 -37.05784 -0.1670074 -0.5856425  0.5415540 -0.5249681
496 496 -36.52155 -37.22485  0.7032977 -0.1670074 -0.5856425  0.5415540
497 497 -36.49747 -36.52155  0.0240795  0.7032977 -0.1670074 -0.5856425
498 498 -35.90126 -36.49747  0.5962114  0.0240795  0.7032977 -0.1670074
499 499 -34.80263 -35.90126  1.0986273  0.5962114  0.0240795  0.7032977
500 500 -34.46493 -34.80263  0.3377050  1.0986273  0.5962114  0.0240795
     Δy_{t-4}
495 -2.5709663
496 -0.5249681
497  0.5415540
498 -0.5856425
499 -0.1670074
500  0.7032977

$result_lm

Call:
lm(formula = adf_model, data = df)

Residuals:
     Min       1Q   Median       3Q      Max 
-3.03779 -0.80930 -0.02605  0.64660  2.69067 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)  
`Δy_{t-1}`  0.07843    0.04509   1.739   0.0826 .
`Δy_{t-2}`  0.02060    0.04478   0.460   0.6456  
`Δy_{t-3}` -0.03174    0.04476  -0.709   0.4785  
`Δy_{t-4}`  0.02337    0.04468   0.523   0.6011  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1.029 on 491 degrees of freedom
Multiple R-squared:  0.008013,  Adjusted R-squared:  -6.85e-05 
F-statistic: 0.9915 on 4 and 491 DF,  p-value: 0.4117


$adf_model
[1] "Δy_t ~ Δy_{t-1} + Δy_{t-2} + Δy_{t-3} + Δy_{t-4} + 0"

# 分散比
r <- 2
k <- 2 + p
Fvalue <- ((ssr_restricted - ssr_unrestricted)/r)/(ssr_unrestricted/(length(unrest_resi) - k))
Fvalue

[1] 1.215123

# Rのur.df {urca}の結果と照合します。
ur.df(y = y, type = "drift", lags = p) %>%
    summary() %>%
    .@teststat
# phi1の結果は一致します。

               tau2     phi1
statistic 0.5494526 1.215123

参考引用文献

Walter Enders(2014),『APPLIED ECONOMETRIC TIME SERIES(FOURTH EDITION)』,WILEY.
村尾博(2019),『Rで学ぶVAR実証分析』,オーム社,pp.123-143

最終更新

Sys.time()

[1] "2024-04-24 11:01:15 JST"

R、Quarto、Package

R.Version()$version.string

[1] "R version 4.3.3 (2024-02-29 ucrt)"

quarto::quarto_version()

[1] '1.4.553'

packageVersion(pkg = "tidyverse")

[1] '2.0.0'

著者

アセット･マネジメント･コンサルティング株式会社 https://www.am-consulting.co.jp
法人概要 https://www.contact.am-consulting.co.jp/company-brochure/
代表取締役三竹道雄 https://www.contact.am-consulting.co.jp/mitake-michio/
公開コンテンツリスト https://www.am-consulting.co.jp/amc-all-contents.html
Charts https://www.am-consulting.co.jp/charts.html
法令検索 https://www.laws.am-consulting.co.jp/
SaECaNet https://www.saecanet.com/
twitter https://twitter.com/amc_corporation
youtube https://www.youtube.com/user/michiomitake
twilog https://twilog.togetter.com/amc_corporation
github https://github.com/am-consulting