はじめに
- 以下に記すRコードは「村尾博(2019),『Rで学ぶVAR実証分析』,オーム社,pp.279-284」を参照引用している。
- VARモデルのVMA表現は各内生変数が定常であることを前提とするが、本ページは一般化インパルス応答関数のアルゴリズム確認を目的とし、本サンプルデータ各系列の定常性は問わない事とする。
サンプルデータ
- 日本のマネタリーベース、米ドル日本円為替レート、日経平均株価の3系列をサンプルデータとする。
- マネタリーベースの単位は兆円。
Date NIKKEI USDJPY MonetaryBase
1 2000-01-01 19539.70 105.16 72.1978
2 2000-02-01 19959.52 109.34 62.6865
3 2000-03-01 20337.32 106.71 64.9807
4 2000-04-01 17973.70 105.48 65.8350
5 2000-05-01 16332.45 108.11 63.7448
6 2000-06-01 17411.05 106.23 62.2152
Date NIKKEI USDJPY MonetaryBase
265 2022-01-01 27001.98 114.83 662.7169
266 2022-02-01 26526.82 115.20 657.1737
267 2022-03-01 27821.43 118.51 662.1323
268 2022-04-01 26847.90 126.04 687.4736
269 2022-05-01 27279.80 128.78 680.0213
270 2022-06-01 26393.04 133.86 673.4841
# 各系列を対数変換
logM <- log(in_data$MonetaryBase)
logU <- log(in_data$USDJPY)
logN <- log(in_data$NIKKEI)
直交化インパルス応答の問題点
直交化インパルス応答のショックは誘導VARモデルの撹乱項の共分散行列\(\,\pmb{\Sigma}_u\,\)をコレスキー分解し、\[\pmb{\Sigma_u}=\textbf{PP}^{'}\]の下三角行列\(\,\textbf{P}\,\)を利用した\(\,\textbf{P}\pmb{e}_j\,\)とするため、行列\(\,\textbf{P}\,\)が下三角行列であるが故に、モデル構造が再帰的構造になっている。
よって、内生変数の並び順でインパルス応答値の結果が変わってくる問題が生じる。直交化インパルス応答値を求める際の内生変数の順序について
一般化インパルス応答関数のショック
そこで一般化インパルス応答関数では、誘導VARモデルの撹乱項の共分散行列\(\,\pmb{\Sigma}_u\,\)の1つの列をそのままショックとして利用する。
所与の1つのショックをスカラー値\(\,u_{jt}=\delta_j\,\)、同ショックから影響を受ける他の要素を\(\,\textbf{u}_{it}\,\,(i\neq j)\,\)とすると、\(\,\textbf{u}_{it}\,\)への影響は期待値\(\,\textrm{E}(\textbf{u}_t|u_{jt}=\delta_j)\,\)で観測できる。
そこで、\(\,\textbf{u}_t\,\)の要素はいずれも正規分布に従うと仮定すれば、同期待値はショック\(\,\delta_j\,\)に対して線形になる。
つまり、\(\,\textrm{E}\left(\textbf{u}_t|u_{jt}=\delta_j\right)\,\)は「\(j\,\)番撹乱項\(\,u_{jt}\,\)と他の撹乱項の共分散からなるベクトル」と「ショックの分散の期待値(=\(\,j\,\)番撹乱項\(\,u_{jt}\,\)の分散)\(\,\sigma_{jj}=\textrm{E}\left(u_{jt}^2\right)\,\)で除して正規化したショック」とを乗じた結果のベクトルとなる。
\[\textrm{E}\left(\textbf{u}_t|u_{jt}=\delta_j\right)=(\sigma_{1j},\sigma_{2j},\cdots,\sigma_{Kj})^{'}\dfrac{\delta_j}{\sigma_{jj}}\]
ここで、\[(\sigma_{1j},\sigma_{2j},\cdots,\sigma_{Kj})^{'}=\textrm{E}(\textbf{u}_t\,u_{jy})=\pmb{\eta}_j\]とすると、\(\textbf{u}_{it}\)への影響は \[\textrm{E}\left(\textbf{u}_t|u_{jt}=\delta_j\right)=\pmb{\eta}_j\sigma_{jj}^{-1}\delta_j\]と表すことが出来る。
さらに\(\,\pmb{\eta}_j\,\)は\(\,\pmb{\Sigma}_u\,\)の\(\,j\,\)列であることを意味し、選択ベクトル\(\,\textbf{e}_j\,\)により\(\,\pmb{\eta}_j=\pmb{\Sigma}_u\textbf{e}_j\,\)の形で取り出すことができる。
従って\[\textrm{E}\left(\textbf{u}_t|u_{jt}=\delta_j\right)=\pmb{\eta}_j\sigma_{jj}^{-1}\delta_j=\pmb{\Sigma}_u\textbf{e}_j\sigma_{jj}^{-1}\delta_j\]
さらにショック\(\,\delta_j\,\)の大きさを\[\dfrac{\delta_j}{\sqrt{\sigma_{jj}}}\]として標準偏差1の大きさで正規化すると
\[\begin{split}
\textrm{E}\left(\textbf{u}_t|u_{jt}=\dfrac{\delta_j}{\sqrt{\sigma_{jj}}}\right)
&=\dfrac{\pmb{\Sigma}_u\textbf{e}_j\sigma_{jj}^{-1}\delta_j}{\dfrac{\delta_j}{\sqrt{\sigma_{jj}}}}\\
&=\pmb{\Sigma}_u\textbf{e}_j\dfrac{\delta_j}{\sigma_{jj}}\dfrac{\sqrt{\sigma_{jj}}}{\delta_j}\\
&=\pmb{\Sigma}_u\textbf{e}_j\dfrac{\sqrt{\sigma_{jj}}}{\sigma_{jj}}\\
&=\pmb{\Sigma}_u\textbf{e}_j\dfrac{1}{\sqrt{\sigma_{jj}}}\\
\end{split}\]となり、これを一般化インパルス応答関数のショックとする。
一般化インパルス応答関数の注意点
直交化インパルス応答は再帰的構造を仮定しており、一般化インパルス応答は撹乱項の正規分布を仮定している。
よって一般化インパルス応答関数によりインパルス応答値を求める場合は、撹乱項が正規分布に従っているか確認する必要がある。
誘導VARモデルの作成
library(vars)
library(dplyr)
y_data_VAR <- data.frame(y1 = logN, y2 = logU, y3 = logM)
VARselect(y = y_data_VAR, lag.max = 12, type = "both")$selection
AIC(n) HQ(n) SC(n) FPE(n)
4 2 1 4
p <- 4
out_VAR <- VAR(y = y_data_VAR, p = p, type = "both")
out_VAR %>%
summary()
VAR Estimation Results:
=========================
Endogenous variables: y1, y2, y3
Deterministic variables: both
Sample size: 266
Log Likelihood: 1719.763
Roots of the characteristic polynomial:
0.9919 0.9191 0.9191 0.7239 0.7239 0.6829 0.5101 0.5101 0.4108 0.4108 0.3712 0.05452
Call:
VAR(y = y_data_VAR, p = p, type = "both")
Estimation results for equation y1:
===================================
y1 = y1.l1 + y2.l1 + y3.l1 + y1.l2 + y2.l2 + y3.l2 + y1.l3 + y2.l3 + y3.l3 + y1.l4 + y2.l4 + y3.l4 + const + trend
Estimate Std. Error t value Pr(>|t|)
y1.l1 1.0354220 0.0659815 15.693 < 0.0000000000000002 ***
y2.l1 0.1229076 0.1727175 0.712 0.47736
y3.l1 -0.0175806 0.1440308 -0.122 0.90295
y1.l2 -0.0929461 0.0923842 -1.006 0.31534
y2.l2 -0.1070396 0.2530410 -0.423 0.67265
y3.l2 0.1013771 0.2132295 0.475 0.63489
y1.l3 0.0759440 0.0931194 0.816 0.41553
y2.l3 -0.0182419 0.2490213 -0.073 0.94166
y3.l3 0.0171747 0.2038242 0.084 0.93291
y1.l4 -0.0717775 0.0651970 -1.101 0.27198
y2.l4 -0.0241272 0.1666939 -0.145 0.88503
y3.l4 -0.0611648 0.1359983 -0.450 0.65328
const 0.4517469 0.1616461 2.795 0.00559 **
trend -0.0001556 0.0001920 -0.811 0.41837
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.05426 on 252 degrees of freedom
Multiple R-Squared: 0.9784, Adjusted R-squared: 0.9773
F-statistic: 877.9 on 13 and 252 DF, p-value: < 0.00000000000000022
Estimation results for equation y2:
===================================
y2 = y1.l1 + y2.l1 + y3.l1 + y1.l2 + y2.l2 + y3.l2 + y1.l3 + y2.l3 + y3.l3 + y1.l4 + y2.l4 + y3.l4 + const + trend
Estimate Std. Error t value Pr(>|t|)
y1.l1 0.07954826 0.02549318 3.120 0.00202 **
y2.l1 1.10653480 0.06673257 16.582 < 0.0000000000000002 ***
y3.l1 0.06823699 0.05564896 1.226 0.22127
y1.l2 -0.05830228 0.03569434 -1.633 0.10364
y2.l2 -0.01079695 0.09776705 -0.110 0.91215
y3.l2 -0.09434271 0.08238514 -1.145 0.25324
y1.l3 -0.02973409 0.03597840 -0.826 0.40933
y2.l3 -0.17648586 0.09621397 -1.834 0.06779 .
y3.l3 0.06219358 0.07875123 0.790 0.43042
y1.l4 0.02826544 0.02519007 1.122 0.26289
y2.l4 0.01320570 0.06440526 0.205 0.83771
y3.l4 -0.02352427 0.05254542 -0.448 0.65476
const 0.08678798 0.06245494 1.390 0.16587
trend -0.00018664 0.00007418 -2.516 0.01249 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.02096 on 252 degrees of freedom
Multiple R-Squared: 0.9742, Adjusted R-squared: 0.9728
F-statistic: 730.9 on 13 and 252 DF, p-value: < 0.00000000000000022
Estimation results for equation y3:
===================================
y3 = y1.l1 + y2.l1 + y3.l1 + y1.l2 + y2.l2 + y3.l2 + y1.l3 + y2.l3 + y3.l3 + y1.l4 + y2.l4 + y3.l4 + const + trend
Estimate Std. Error t value Pr(>|t|)
y1.l1 0.00939876 0.02708309 0.347 0.729
y2.l1 0.06917772 0.07089443 0.976 0.330
y3.l1 1.18212525 0.05911957 19.995 < 0.0000000000000002 ***
y1.l2 -0.05164806 0.03792046 -1.362 0.174
y2.l2 0.00906665 0.10386440 0.087 0.931
y3.l2 -0.36887356 0.08752319 -4.215 0.000034892071 ***
y1.l3 -0.01053272 0.03822224 -0.276 0.783
y2.l3 -0.01673553 0.10221446 -0.164 0.870
y3.l3 0.53148908 0.08366264 6.353 0.000000000982 ***
y1.l4 0.03748010 0.02676108 1.401 0.163
y2.l4 -0.03564392 0.06842197 -0.521 0.603
y3.l4 -0.35037770 0.05582248 -6.277 0.000000001501 ***
const 0.04358780 0.06635002 0.657 0.512
trend 0.00012521 0.00007881 1.589 0.113
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 0.02227 on 252 degrees of freedom
Multiple R-Squared: 0.9992, Adjusted R-squared: 0.9992
F-statistic: 2.471e+04 on 13 and 252 DF, p-value: < 0.00000000000000022
Covariance matrix of residuals:
y1 y2 y3
y1 0.00294404 0.0003450 0.00001276
y2 0.00034496 0.0004395 0.00006190
y3 0.00001276 0.0000619 0.00049602
Correlation matrix of residuals:
y1 y2 y3
y1 1.00000 0.3033 0.01056
y2 0.30327 1.0000 0.13257
y3 0.01056 0.1326 1.00000
誘導VARモデルから係数行列\(\,\textbf{B}\,\)を確認する。
B_whole <- Bcoef(out_VAR)
B_whole
y1.l1 y2.l1 y3.l1 y1.l2 y2.l2 y3.l2
y1 1.035422041 0.12290761 -0.01758064 -0.09294606 -0.107039552 0.10137713
y2 0.079548258 1.10653480 0.06823699 -0.05830228 -0.010796951 -0.09434271
y3 0.009398758 0.06917772 1.18212525 -0.05164806 0.009066648 -0.36887356
y1.l3 y2.l3 y3.l3 y1.l4 y2.l4 y3.l4
y1 0.07594398 -0.01824187 0.01717468 -0.07177746 -0.02412722 -0.06116478
y2 -0.02973409 -0.17648586 0.06219358 0.02826544 0.01320570 -0.02352427
y3 -0.01053272 -0.01673553 0.53148908 0.03748010 -0.03564392 -0.35037770
const trend
y1 0.45174689 -0.0001556285
y2 0.08678798 -0.0001866442
y3 0.04358780 0.0001252077
B_1 <- B_whole[, 1:3]
B_2 <- B_whole[, 4:6]
B_3 <- B_whole[, 7:9]
B_4 <- B_whole[, 10:12]
B_z <- B_whole[, 13:14]
y1.l1 y2.l1 y3.l1
y1 1.035422041 0.12290761 -0.01758064
y2 0.079548258 1.10653480 0.06823699
y3 0.009398758 0.06917772 1.18212525
const trend
y1 0.45174689 -0.0001556285
y2 0.08678798 -0.0001866442
y3 0.04358780 0.0001252077
誘導撹乱項の共分散行列
sigma_cov <- summary(out_VAR)$covres
sigma_cov
y1 y2 y3
y1 0.00294403830 0.00034496330 0.00001275781
y2 0.00034496330 0.00043948752 0.00006189729
y3 0.00001275781 0.00006189729 0.00049601525
選択ベクトル
- ショックはマネタリーベースの撹乱項に発生する設定とする。
select <- c(0, 0, 1)
select
インパルス応答値の算出
# ショックの大きさを調整するスケールファクター
scale_factor <- 1
# 一般化インパルス応答関数のショック
sigma_pick <- sigma_u[3, 3] # マネタリーベース撹乱項の分散
sqrt_sigma <- sqrt(sigma_pick)
shock_gen <- (sigma_u/sqrt_sigma) %*% select * scale_factor
shock_gen
[,1]
y1 0.000572834
y2 0.002779228
y3 0.022271400
# 分析条件設定
num_y <- 3 # 内生変数の数
num_z <- 2 # 外生変数(ドリフト項、トレンド項)の数
num_lag <- 4 # ラグ次数
num_x <- num_lag * num_y + num_z
num_h <- 50 # 観測期数
num_col <- num_h + num_lag
# インパルス応答値(y)と外生変数の初期設定
y <- matrix(0, nrow = num_y, ncol = num_col)
z <- matrix(0, nrow = num_z, ncol = num_col)
h <- num_lag + 1
y[, h] <- shock_gen
for (h in (num_lag + 2):num_col) {
y[, h] <- B_1 %*% y[, h - 1] + B_2 %*% y[, h - 2] + B_3 %*% y[, h - 3] + B_4 %*% y[, h - 4] + B_z %*% z[, h]
print(y[, h])
}
[1] 0.0005431677 0.0046406135 0.0265252287
[1] 0.002573525 0.004823661 0.023462557
[1] 0.005362208 0.005436659 0.030107585
[1] 0.006255852 0.006424734 0.033407021
[1] 0.007388717 0.006658709 0.031584341
[1] 0.009120080 0.006863333 0.032837061
[1] 0.010085892 0.007351197 0.034446377
[1] 0.010822426 0.007628696 0.033699600
[1] 0.011827237 0.007798292 0.033520734
[1] 0.012604018 0.008085638 0.034026081
[1] 0.013163587 0.008334896 0.033711897
[1] 0.013783668 0.008508834 0.033309954
[1] 0.014340773 0.008709996 0.033291802
[1] 0.01476461 0.00890925 0.03307207
[1] 0.01516671 0.00906788 0.03270894
[1] 0.015540152 0.009220567 0.032494382
[1] 0.015839238 0.009371086 0.032264930
[1] 0.01609827 0.00949984 0.03195403
[1] 0.016331998 0.009614894 0.031684540
[1] 0.016522177 0.009723138 0.031434702
[1] 0.016676346 0.009817627 0.031153135
[1] 0.016806290 0.009898868 0.030878022
[1] 0.016907779 0.009971051 0.030618885
[1] 0.01698179 0.01003273 0.03035196
[1] 0.01703481 0.01008331 0.03008450
[1] 0.01706757 0.01012480 0.02982589
[1] 0.01708041 0.01015750 0.02956808
[1] 0.01707658 0.01018120 0.02931033
[1] 0.01705786 0.01019682 0.02905737
[1] 0.01702495 0.01020502 0.02880740
[1] 0.01697961 0.01020596 0.02855887
[1] 0.01692341 0.01020019 0.02831352
[1] 0.01685723 0.01018828 0.02807130
[1] 0.01678220 0.01017058 0.02783131
[1] 0.01669947 0.01014749 0.02759397
[1] 0.01660991 0.01011949 0.02735949
[1] 0.01651431 0.01008694 0.02712749
[1] 0.01641350 0.01005020 0.02689798
[1] 0.01630819 0.01000964 0.02667106
[1] 0.016198980 0.009965598 0.026446602
[1] 0.016086470 0.009918377 0.026224519
[1] 0.015971192 0.009868282 0.026004838
[1] 0.015853604 0.009815597 0.025787496
[1] 0.01573414 0.00976058 0.02557242
[1] 0.015613175 0.009703477 0.025359580
[1] 0.015491060 0.009644522 0.025148943
[1] 0.015368097 0.009583926 0.024940446
[1] 0.015244560 0.009521887 0.024734051
[1] 0.01512069 0.00945859 0.02452972
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8]
[1,] 0 0 0 0 0.000572834 0.0005431677 0.002573525 0.005362208
[2,] 0 0 0 0 0.002779228 0.0046406135 0.004823661 0.005436659
[3,] 0 0 0 0 0.022271400 0.0265252287 0.023462557 0.030107585
[,9] [,10]
[1,] 0.006255852 0.007388717
[2,] 0.006424734 0.006658709
[3,] 0.033407021 0.031584341
[,1] [,2] [,3] [,4] [,5] [,6]
[1,] 0.016198980 0.016086470 0.015971192 0.015853604 0.01573414 0.015613175
[2,] 0.009965598 0.009918377 0.009868282 0.009815597 0.00976058 0.009703477
[3,] 0.026446602 0.026224519 0.026004838 0.025787496 0.02557242 0.025359580
[,7] [,8] [,9] [,10]
[1,] 0.015491060 0.015368097 0.015244560 0.01512069
[2,] 0.009644522 0.009583926 0.009521887 0.00945859
[3,] 0.025148943 0.024940446 0.024734051 0.02452972
out_y <- y[, (num_lag - 1):num_col]
irf_gen <- t(out_y)
y_min <- min(irf_gen)
y_max <- max(irf_gen)
x_data <- matrix(-1:num_h, nrow = (num_h + 2), ncol = 1)
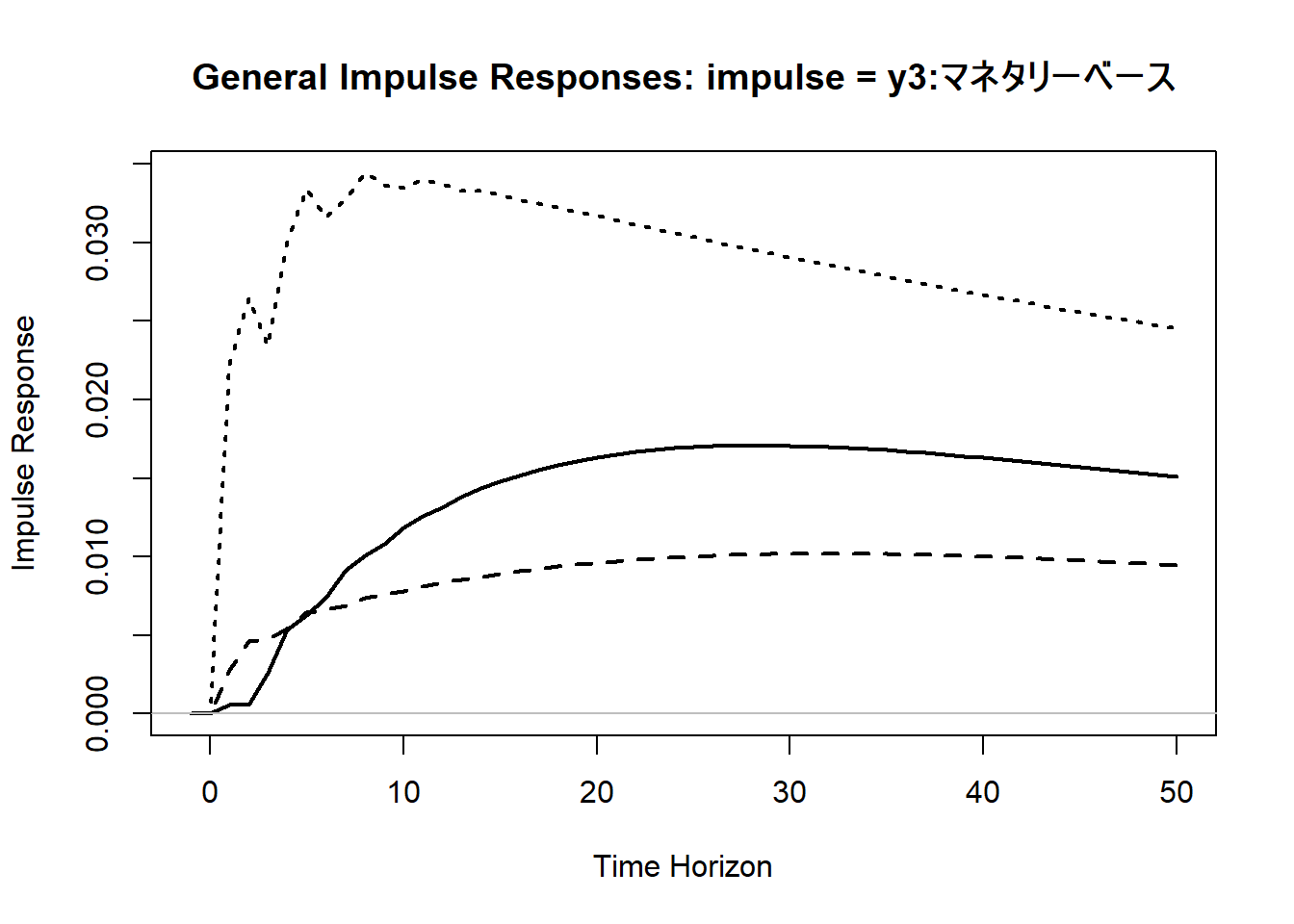
matplot(x_data, irf_gen, type = "l", lwd = 2, col = 1, lty = c("solid", "dashed", "dotted"), xlim = c(-1, num_h), ylim = c(y_min, y_max), xlab = "Time Horizon", ylab = "Impulse Response", main = "General Impulse Responses: impulse = y3:マネタリーベース")
abline(h = 0, col = "gray")
実線:y1 日経平均株価、破線:y2 ドル円為替レート、点線:y3 マネタリーベース
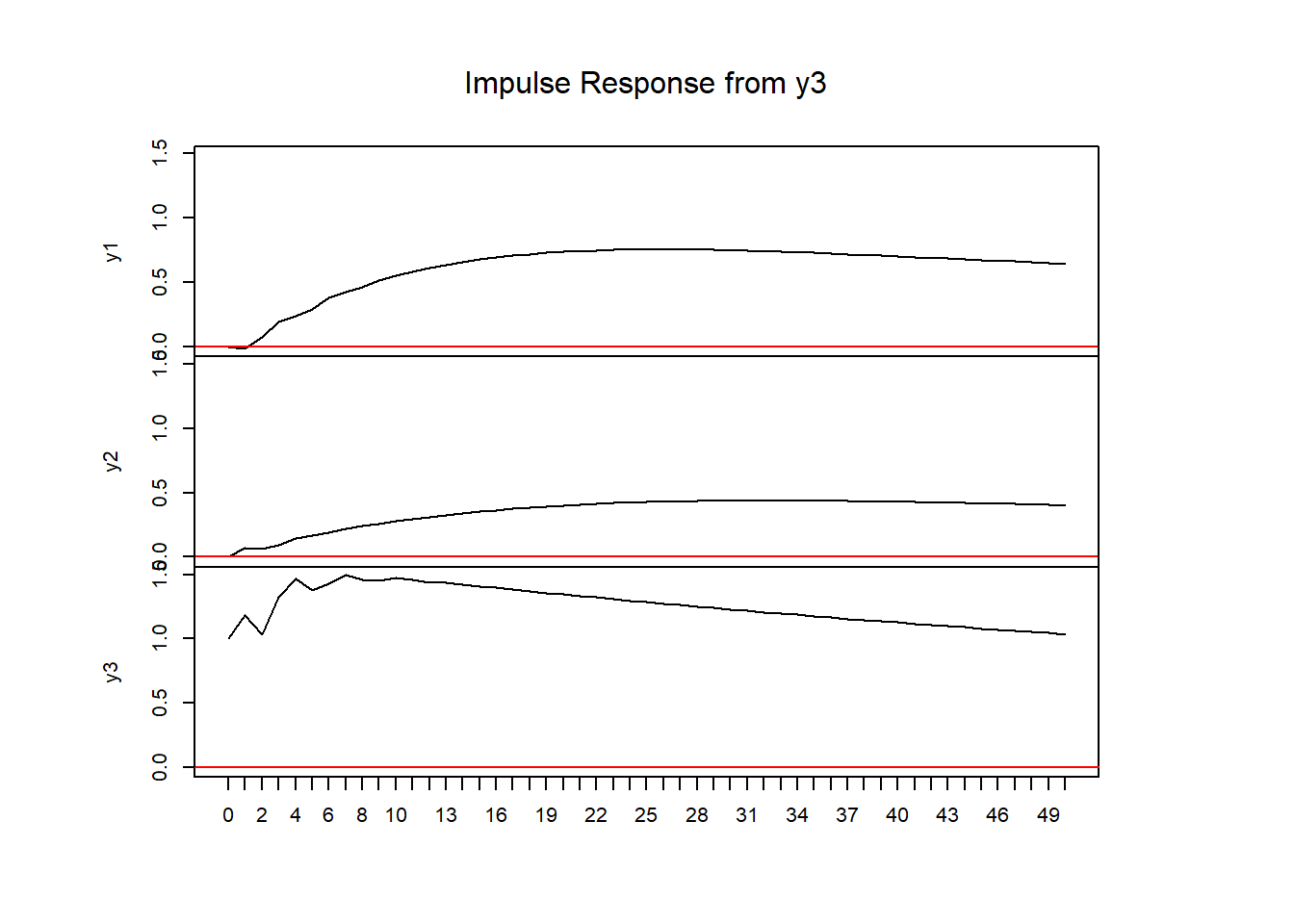
関数irf {vars}によるインパルス応答
irf(x = out_VAR, impulse = "y3", n.ahead = 50, ortho = F, boot = F) %>%
plot()
参照引用資料
- 村尾博(2019),『Rで学ぶVAR実証分析』,オーム社,pp.265-271
最終更新
[1] "2024-04-15 06:50:19 JST"
R、Quarto、Package
R.Version()$version.string
[1] "R version 4.3.3 (2024-02-29 ucrt)"
packageVersion(pkg = "tidyverse")