Rで時系列分析:直交化インパルス応答関数

Rでデータサイエンス

はじめに

  • 以下に記すRコードは「村尾博(2019),『Rで学ぶVAR実証分析』,オーム社,pp.279-284」を参照引用している。
  • VARモデルのVMA表現は各内生変数が定常であることを前提とするが、本ページは直交化インパルス応答関数のアルゴリズム確認を目的とし、本サンプルデータ各系列の定常性は問わない事とする。

サンプルデータ

  • 日本のマネタリーベース、米ドル日本円為替レート、日経平均株価の3系列をサンプルデータとする。
  • マネタリーベースの単位は兆円。
head(in_data)
        Date   NIKKEI USDJPY MonetaryBase
1 2000-01-01 19539.70 105.16      72.1978
2 2000-02-01 19959.52 109.34      62.6865
3 2000-03-01 20337.32 106.71      64.9807
4 2000-04-01 17973.70 105.48      65.8350
5 2000-05-01 16332.45 108.11      63.7448
6 2000-06-01 17411.05 106.23      62.2152
tail(in_data)
          Date   NIKKEI USDJPY MonetaryBase
265 2022-01-01 27001.98 114.83     662.7169
266 2022-02-01 26526.82 115.20     657.1737
267 2022-03-01 27821.43 118.51     662.1323
268 2022-04-01 26847.90 126.04     687.4736
269 2022-05-01 27279.80 128.78     680.0213
270 2022-06-01 26393.04 133.86     673.4841
nrow(in_data)
[1] 270
# 各系列を対数変換
logM <- log(in_data$MonetaryBase)
logU <- log(in_data$USDJPY)
logN <- log(in_data$NIKKEI)

構造VARモデルと誘導VARモデル

次の構造VARモデルと誘導VARモデルを考える。

\[\begin{split} \textbf{Ay}_t&=\textbf{A}_1\textbf{y}_{t-1}+\textbf{A}_2\textbf{y}_{t-2}+\pmb{\epsilon}_t\\ \textbf{y}_t&=\textbf{B}_1\textbf{y}_{t-1}+\textbf{B}_2\textbf{y}_{t-2}+\textbf{u}_t \end{split}\]

ここで、\(\,\textbf{B}_i=\textbf{A}^{-1}\textbf{A}_i\,\,(i=1,2),\quad\textbf{u}_t=\textbf{A}^{-1}\pmb{\epsilon}_t\,\)である。

内生変数は同時点における「相互依存関係」を想定しているが、この通り、誘導VARモデルでは同時点の相互依存関係を無視することになり、構造VARモデルならば内生変数の相互依存関係を反映することが出来る。

なお、構造撹乱項\(\,\pmb{\epsilon}_t\,\)は以下の性質を持つ。

『異なった時点間では相関を持たず，また，同時点での相関関係もない，平均がゼロの同一な分布にしたがって発生する確率変数として捉えられる性質のものであるとする。これは，経済に発生するショックは，その本源的な段階まで遡れば，相互に独立したショックから成っているという考え方に基づいている。もし，２つのショックの間に相関関係があれば，それは２つのショックが共通のさらに本源的なショックを含んでいるためであると考えるのである。』 https://dl.ndl.go.jp/view/download/digidepo_11172758_po_r_59_074_140.pdf?contentNo=1&alternativeNo=#page=4

『なお、直交化インパルス応答における「直交化」は、構造撹乱項が互いに無相関、つまり互いに直交の関係になっていることに由来する。具体的には構造撹乱項の共分散行列が対角行列になっていることに由来する』(村尾博(2019),『Rで学ぶVAR実証分析』,オーム社,p.262)

誘導VARモデルの作成

library(vars)
library(dplyr)
y_data_VAR <- data.frame(y1 = logN, y2 = logU, y3 = logM)
VARselect(y = y_data_VAR, lag.max = 12, type = "both")$selection
AIC(n)  HQ(n)  SC(n) FPE(n) 
     4      2      1      4 
p <- 4
out_VAR <- VAR(y = y_data_VAR, p = p, type = "both")
out_VAR %>%
    summary()

VAR Estimation Results:
========================= 
Endogenous variables: y1, y2, y3 
Deterministic variables: both 
Sample size: 266 
Log Likelihood: 1719.763 
Roots of the characteristic polynomial:
0.9919 0.9191 0.9191 0.7239 0.7239 0.6829 0.5101 0.5101 0.4108 0.4108 0.3712 0.05452
Call:
VAR(y = y_data_VAR, p = p, type = "both")


Estimation results for equation y1: 
=================================== 
y1 = y1.l1 + y2.l1 + y3.l1 + y1.l2 + y2.l2 + y3.l2 + y1.l3 + y2.l3 + y3.l3 + y1.l4 + y2.l4 + y3.l4 + const + trend 

        Estimate Std. Error t value             Pr(>|t|)    
y1.l1  1.0354220  0.0659815  15.693 < 0.0000000000000002 ***
y2.l1  0.1229076  0.1727175   0.712              0.47736    
y3.l1 -0.0175806  0.1440308  -0.122              0.90295    
y1.l2 -0.0929461  0.0923842  -1.006              0.31534    
y2.l2 -0.1070396  0.2530410  -0.423              0.67265    
y3.l2  0.1013771  0.2132295   0.475              0.63489    
y1.l3  0.0759440  0.0931194   0.816              0.41553    
y2.l3 -0.0182419  0.2490213  -0.073              0.94166    
y3.l3  0.0171747  0.2038242   0.084              0.93291    
y1.l4 -0.0717775  0.0651970  -1.101              0.27198    
y2.l4 -0.0241272  0.1666939  -0.145              0.88503    
y3.l4 -0.0611648  0.1359983  -0.450              0.65328    
const  0.4517469  0.1616461   2.795              0.00559 ** 
trend -0.0001556  0.0001920  -0.811              0.41837    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1


Residual standard error: 0.05426 on 252 degrees of freedom
Multiple R-Squared: 0.9784, Adjusted R-squared: 0.9773 
F-statistic: 877.9 on 13 and 252 DF,  p-value: < 0.00000000000000022 


Estimation results for equation y2: 
=================================== 
y2 = y1.l1 + y2.l1 + y3.l1 + y1.l2 + y2.l2 + y3.l2 + y1.l3 + y2.l3 + y3.l3 + y1.l4 + y2.l4 + y3.l4 + const + trend 

         Estimate  Std. Error t value             Pr(>|t|)    
y1.l1  0.07954826  0.02549318   3.120              0.00202 ** 
y2.l1  1.10653480  0.06673257  16.582 < 0.0000000000000002 ***
y3.l1  0.06823699  0.05564896   1.226              0.22127    
y1.l2 -0.05830228  0.03569434  -1.633              0.10364    
y2.l2 -0.01079695  0.09776705  -0.110              0.91215    
y3.l2 -0.09434271  0.08238514  -1.145              0.25324    
y1.l3 -0.02973409  0.03597840  -0.826              0.40933    
y2.l3 -0.17648586  0.09621397  -1.834              0.06779 .  
y3.l3  0.06219358  0.07875123   0.790              0.43042    
y1.l4  0.02826544  0.02519007   1.122              0.26289    
y2.l4  0.01320570  0.06440526   0.205              0.83771    
y3.l4 -0.02352427  0.05254542  -0.448              0.65476    
const  0.08678798  0.06245494   1.390              0.16587    
trend -0.00018664  0.00007418  -2.516              0.01249 *  
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1


Residual standard error: 0.02096 on 252 degrees of freedom
Multiple R-Squared: 0.9742, Adjusted R-squared: 0.9728 
F-statistic: 730.9 on 13 and 252 DF,  p-value: < 0.00000000000000022 


Estimation results for equation y3: 
=================================== 
y3 = y1.l1 + y2.l1 + y3.l1 + y1.l2 + y2.l2 + y3.l2 + y1.l3 + y2.l3 + y3.l3 + y1.l4 + y2.l4 + y3.l4 + const + trend 

         Estimate  Std. Error t value             Pr(>|t|)    
y1.l1  0.00939876  0.02708309   0.347                0.729    
y2.l1  0.06917772  0.07089443   0.976                0.330    
y3.l1  1.18212525  0.05911957  19.995 < 0.0000000000000002 ***
y1.l2 -0.05164806  0.03792046  -1.362                0.174    
y2.l2  0.00906665  0.10386440   0.087                0.931    
y3.l2 -0.36887356  0.08752319  -4.215       0.000034892071 ***
y1.l3 -0.01053272  0.03822224  -0.276                0.783    
y2.l3 -0.01673553  0.10221446  -0.164                0.870    
y3.l3  0.53148908  0.08366264   6.353       0.000000000982 ***
y1.l4  0.03748010  0.02676108   1.401                0.163    
y2.l4 -0.03564392  0.06842197  -0.521                0.603    
y3.l4 -0.35037770  0.05582248  -6.277       0.000000001501 ***
const  0.04358780  0.06635002   0.657                0.512    
trend  0.00012521  0.00007881   1.589                0.113    
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1


Residual standard error: 0.02227 on 252 degrees of freedom
Multiple R-Squared: 0.9992, Adjusted R-squared: 0.9992 
F-statistic: 2.471e+04 on 13 and 252 DF,  p-value: < 0.00000000000000022 



Covariance matrix of residuals:
           y1        y2         y3
y1 0.00294404 0.0003450 0.00001276
y2 0.00034496 0.0004395 0.00006190
y3 0.00001276 0.0000619 0.00049602

Correlation matrix of residuals:
        y1     y2      y3
y1 1.00000 0.3033 0.01056
y2 0.30327 1.0000 0.13257
y3 0.01056 0.1326 1.00000

誘導VARモデルから係数行列\(\,\textbf{B}\,\)を確認する。

B_whole <- Bcoef(out_VAR)
B_whole
         y1.l1      y2.l1       y3.l1       y1.l2        y2.l2       y3.l2
y1 1.035422041 0.12290761 -0.01758064 -0.09294606 -0.107039552  0.10137713
y2 0.079548258 1.10653480  0.06823699 -0.05830228 -0.010796951 -0.09434271
y3 0.009398758 0.06917772  1.18212525 -0.05164806  0.009066648 -0.36887356
         y1.l3       y2.l3      y3.l3       y1.l4       y2.l4       y3.l4
y1  0.07594398 -0.01824187 0.01717468 -0.07177746 -0.02412722 -0.06116478
y2 -0.02973409 -0.17648586 0.06219358  0.02826544  0.01320570 -0.02352427
y3 -0.01053272 -0.01673553 0.53148908  0.03748010 -0.03564392 -0.35037770
        const         trend
y1 0.45174689 -0.0001556285
y2 0.08678798 -0.0001866442
y3 0.04358780  0.0001252077
B_1 <- B_whole[, 1:3]
B_2 <- B_whole[, 4:6]
B_3 <- B_whole[, 7:9]
B_4 <- B_whole[, 10:12]
B_z <- B_whole[, 13:14]
B_1
         y1.l1      y2.l1       y3.l1
y1 1.035422041 0.12290761 -0.01758064
y2 0.079548258 1.10653480  0.06823699
y3 0.009398758 0.06917772  1.18212525
B_z
        const         trend
y1 0.45174689 -0.0001556285
y2 0.08678798 -0.0001866442
y3 0.04358780  0.0001252077

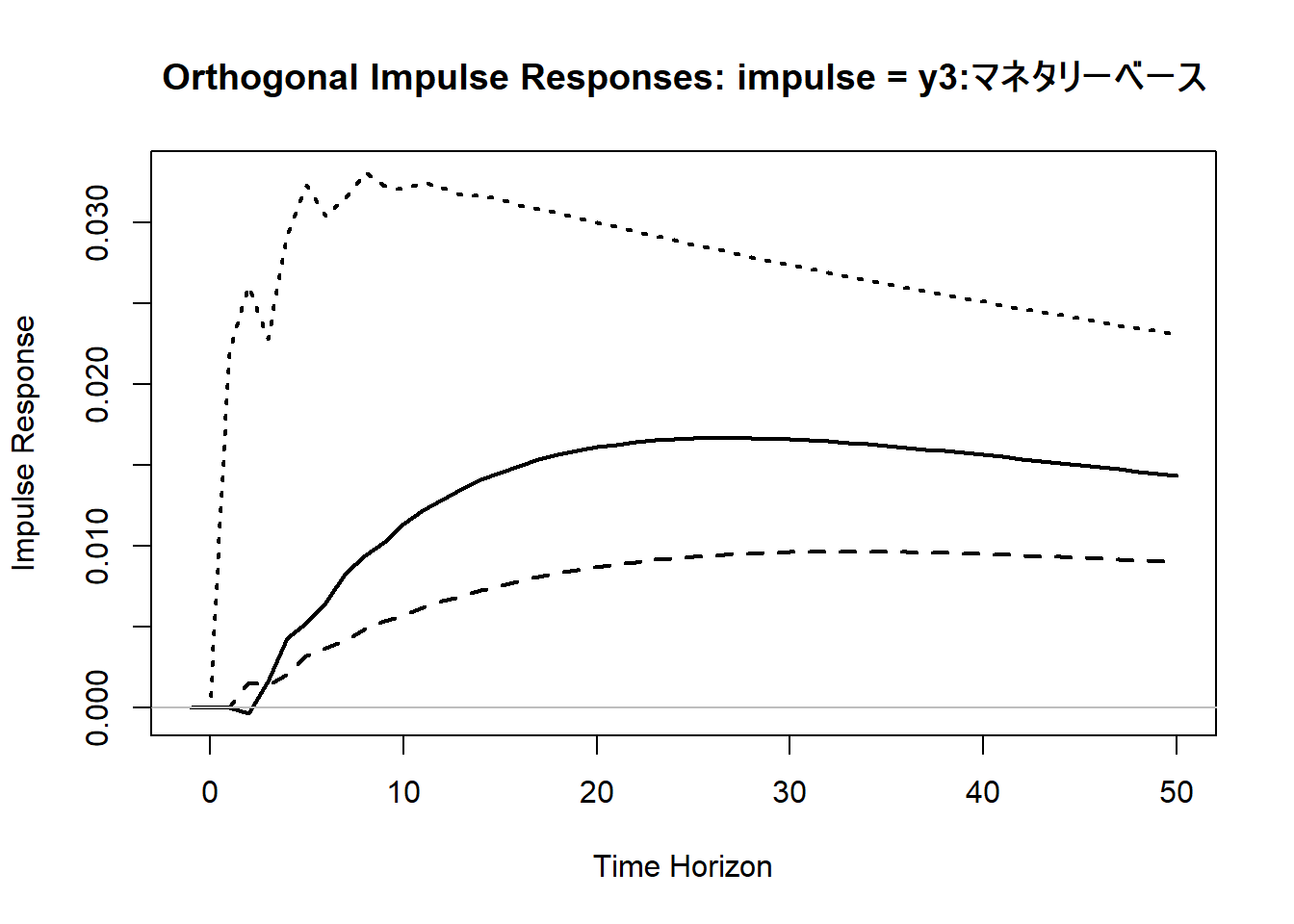
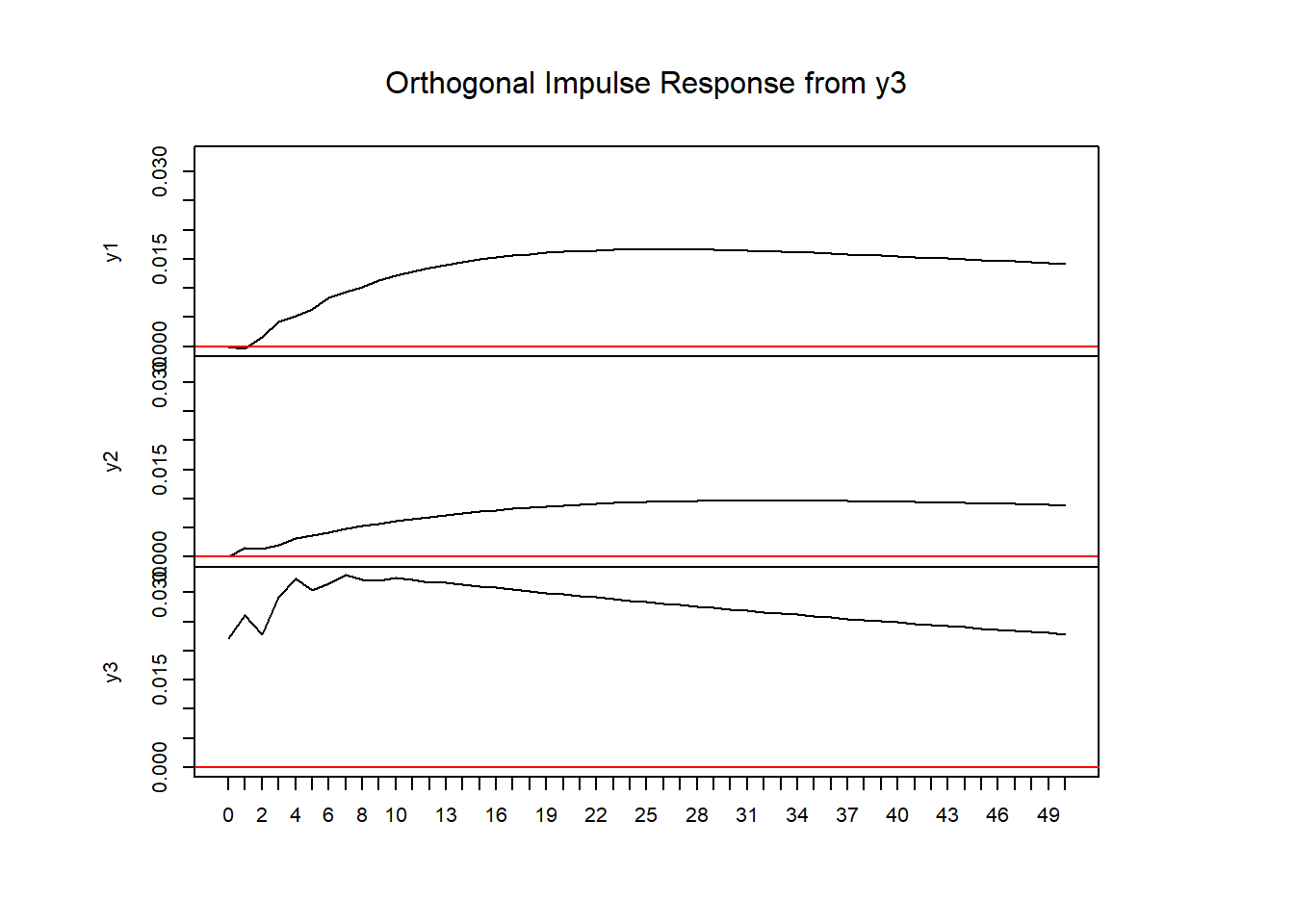
インパルス応答分析のアルゴリズム

時点\(\,h=0\,\)において、構造VARモデルの撹乱項に定数値からなる\(\,K\times1\,\)のベクトル\(\,\delta\,\)が発生したとする。

このとき、ショック\(\,\delta\,\)の内生変数\(\,\textbf{y}_t\,\)への波及(限界)効果(内生変数\(\,\textbf{y}\,\)の変化分)をインパルス応答値\(\,\Delta\textbf{y}\,\)と呼び、その動的変化を調べることがインパルス応答分析である。

前述の通り構造VARモデルの\(\,h=0\,\)時点に外生的なショック\(\,\pmb{\delta}\,\)が撹乱項を通じて同モデルに伝わった場合、インパルス応答値\(\,\Delta\textbf{y}\,\)は以下のように変化する。

時点 インパルス応答値
\(t=-1\) \(\Delta\textbf{y}_{-1}=0\)
\(t=0\) \(\textbf{A}\Delta\textbf{y}_0=\pmb{\delta}\)
\(t=1\) \(\textbf{A}\Delta\textbf{y}_1=\textbf{A}_1\Delta\textbf{y}_0\)
\(t=2\) \(\textbf{A}\Delta\textbf{y}_2=\textbf{A}_1\Delta\textbf{y}_1+\textbf{A}_2\Delta\textbf{y}_0\)
\(t=3\) \(\textbf{A}\Delta\textbf{y}_3=\textbf{A}_1\Delta\textbf{y}_2+\textbf{A}_2\Delta\textbf{y}_1\)
\(\vdots\) \(\vdots\)
\(t=h\) \(\textbf{A}\Delta\textbf{y}_h=\textbf{A}_1\Delta\textbf{y}_{h-1}+\textbf{A}_2\Delta\textbf{y}_{h-2}\)


上表を誘導VARモデルの視点に直すと、

時点 インパルス応答値
\(t=-1\) \(\Delta\textbf{y}_{-1}=0\)
\(t=0\) \(\Delta\textbf{y}_0=\textbf{A}^{-1}\pmb{\delta}\)
\(t=1\) \(\Delta\textbf{y}_1=\textbf{A}^{-1}\textbf{A}_1\Delta\textbf{y}_0=\textbf{B}_1\Delta\textbf{y}_0\)
\(t=2\) \(\Delta\textbf{y}_2=\textbf{A}^{-1}\textbf{A}_1\Delta\textbf{y}_1+\textbf{A}^{-1}\textbf{A}_2\Delta\textbf{y}_0=\textbf{B}_1\Delta\textbf{y}_1+\textbf{B}_2\Delta\textbf{y}_0\)
\(t=3\) \(\Delta\textbf{y}_3=\textbf{A}^{-1}\textbf{A}_1\Delta\textbf{y}_2+\textbf{A}^{-1}\textbf{A}_2\Delta\textbf{y}_1=\textbf{B}_1\Delta\textbf{y}_2+\textbf{B}_2\Delta\textbf{y}_1\)
\(\vdots\) \(\vdots\)
\(t=h\) \(\Delta\textbf{y}_h=\textbf{A}^{-1}\textbf{A}_1\Delta\textbf{y}_{h-1}+\textbf{A}^{-1}\textbf{A}_2\Delta\textbf{y}_{h-2}=\textbf{B}_1\Delta\textbf{y}_{h-1}+\textbf{B}_2\Delta\textbf{y}_{h-2}\)


と表され、これは\(\,\textbf{A}^{-1}\pmb{\delta}\,\)で表現されるショックを\(\,t=0\,\)時点の誘導VARモデルに与え、上表の時点の順に逐次的にインパルス応答値を求めることは、構造VARモデルに基づくインパルス応答値を求めている事と同じである事を表している。

そこで次に\(\,\textbf{A}^{-1}\pmb{\delta}\,\)で表現される誘導VARモデルへのショックを決めることになる。

\(K\times K\,\)の対称な正値定符号行列\(\,\textbf{Q}\,\)はコレスキー分解により\[\textbf{Q}=\textbf{P}\textbf{P}^{'}\]を満たすユニークな下三角行列に分解され、修正コレスキー分解により\(\,\textbf{L}\,\)を対角要素が1の下三角行列、\(\,\textbf{D}\,\)を正の要素を持つ対角行列として\[\textbf{Q}=\textbf{L}\textbf{D}\textbf{L}^{'}\]と分解できる。

ここで、\[\textbf{L}\textbf{D}^{1/2}\left(\textbf{L}\textbf{D}^{1/2}\right)^{'}=\textbf{L}\textbf{D}^{1/2}\left(\textbf{D}^{1/2}\right)^{'}\textbf{L}^{'}=\textbf{L}\textbf{D}^{1/2}\textbf{D}^{1/2}\textbf{L}^{'}=\textbf{L}\textbf{D}\textbf{L}^{'}=\textbf{Q}=\textbf{P}\textbf{P}^{'}\]であること、かつ\(\,\textbf{P}\,\)は一意であることから\[\textbf{P}=\textbf{L}\textbf{D}^{1/2}\]となる。

前述のコレスキー分解、修正コレスキー分解を誘導撹乱項\(\,\textbf{u}_t\,\)の共分散行列\(\,\pmb{\Sigma}_u\)に適用すると\[\pmb{\Sigma}_u=\textbf{P}\textbf{P}^{'}=\textbf{L}\textbf{D}\textbf{L}^{'}\]となるが、2つの撹乱項ベクトルの通り、

\[\pmb{\Sigma}_u=\textbf{A}^{-1}\pmb{\Sigma}_\epsilon\left(\textbf{A}^{-1}\right)^{'}\] であり、 \[\pmb{\Sigma}_u=\textbf{L}\textbf{D}\textbf{L}^{'}\]でもあるため、\(\,\textbf{A}^{-1}=\textbf{L}\,\)と制約した場合、\(\,\pmb{\Sigma}_\epsilon=\textbf{D}\,\)となり、 \[\textbf{P}=\textbf{LD}^{1/2}=\textbf{A}^{-1}\textbf{D}^{1/2}=\textbf{A}^{-1}\pmb{\Sigma}_{\epsilon}^{1/2}=\textbf{A}^{-1}\pmb{\delta}\]となる。

さらに\(\,\textbf{D}\,\)の対角要素は全て正であるため、\(\textbf{D}^{1/2}=\textrm{diag}\left(\sqrt{d_1},\sqrt{d_2},\cdots,\sqrt{d_N}\right)\)となり、つまり\(\,\textbf{P}\,\)は、

  1. 修正コレスキー分解\(\,\pmb{\Sigma}_u=\textbf{LDL}^{-1}\,\)を利用して求めた\(\,\textbf{L}\,\)に設けた \(\,\textbf{A}^{-1}=\textbf{L}\,\)の制約の下では、対角要素が1である下三角行列\(\,\textbf{L}\,\)に、構造撹乱項\(\,\pmb{\epsilon}_t\,\)の分散の平方根である標準偏差を対角要素とする対角行列を乗じた、構造撹乱項の標準偏差を対角要素とする下三角行列となり、再帰的構造VARを構成し、
  2. コレスキー分解\(\,\pmb{\sum}_u=\textbf{PP}^{'}\,\)で求めた誘導撹乱項の共分散行列\(\,\pmb{\sum}_u\,\)の対角要素の平方根である\(\,\textbf{u}\,\)の標準偏差を対角要素とする下三角行列となり、ショックである\(\,\textbf{A}^{-1}\pmb{\delta}\,\)に下三角行列\(\,\textbf{P}\,\)の制約を設けたのが直交化インパルス応答といえる。

続いて期待値、分散を以下の通りに設定する標準化構造撹乱項\(\,\pmb{\epsilon}_t^{\textrm{SD}}\,\)を考える。

\[\textrm{E}\left(\pmb{\epsilon}_t^{\textrm{SD}}\right)=0,\quad\textrm{Var}\left(\pmb{\epsilon}_t^{\textrm{SD}}\right)=\textrm{E}\left[\pmb{\epsilon}_t^{\textrm{SD}}\left(\pmb{\epsilon}_t^{\textrm{SD}}\right)^{'}\right]=\textbf{I}_K,\quad \pmb{\epsilon}_t=\textbf{D}^{1/2}\pmb{\epsilon}_t^{\textrm{SD}}\]

ここで、\(\,\pmb{\epsilon}_t^{\textrm{SD}}\,\)は\(\,K\times 1\,\)のベクトルである。

\(\textbf{u}_t\)を標準化構造撹乱項\(\,\pmb{\epsilon}_t^{\textrm{SD}}\,\)で表現すると、

\[ \begin{split} \textbf{u}_t&=\textbf{A}^{-1}\pmb{\epsilon}_t\\ &=\textbf{A}^{-1}\textbf{D}^{1/2}\pmb{\epsilon}_t^{\textrm{SD}}\\ &=\textbf{L}\textbf{D}^{1/2}\pmb{\epsilon}_t^{\textrm{SD}}\\ &=\textbf{P}\pmb{\epsilon}_t^{\textrm{SD}} \end{split} \] となる。

外生的なショックは1つの内生変数の撹乱項のみに1期だけ発生する想定とする。つまり、\(\,\pmb{\epsilon}_t^{\textrm{SD}}\,\)における\(\,j\,\)番目の要素\(\,\pmb{\epsilon}_{jt}^{\textrm{SD}}=1\,\)と設定し、その他の要素は\(\,0\,\)に設定する。

そのために、\(j\)番目の要素を\(\,1\,\)、他の要素を\(\,0\,\)とする\(\,K\times 1\,\)の選択ベクトル\(\,\textbf{e}_j\,\)を利用する。内生変数が3つ\(\,K=3\,\)の場合は、\(\,\textbf{e}_1=(1,0,0)^{'},\quad\textbf{e}_3=(0,0,1)^{'}\)となる。

単位ショック\(\,\pmb{\epsilon}_{jt}^{\textrm{SD}}=1\,\)の設定は

\[\textbf{P}\pmb{\epsilon}_{jt}^{\textrm{SD}}=\textbf{Pe}_j\]と表現でき、結論として誘導VARモデルには\(\,\textbf{u}_t=\textbf{Pe}_j\,\)のショックを与えることになる。

誘導撹乱項の共分散行列

誘導VARモデルの残差の不偏共分散行列

  • 自由度を\(\,n-1\,\)とした不偏共分散行列。
  • こちらは\(\,\pmb{\Sigma}_u\,\)として利用しない。
# VARモデルの残差
resid <- residuals(out_VAR)
head(resid)
           y1           y2           y3
1 -0.04806574  0.025515018  0.034835170
2  0.08888641 -0.025783526 -0.021916713
3 -0.06822938 -0.008272510  0.016565578
4  0.11178784 -0.008597766 -0.009223917
5 -0.05218443 -0.028379783  0.007406912
6 -0.04108704  0.005229638  0.011092452
tail(resid)
              y1          y2           y3
261 -0.062597728 0.002915330 -0.003472774
262 -0.008596586 0.004264241 -0.015906095
263  0.045869217 0.030042008  0.003802322
264 -0.035629169 0.052424314  0.018437758
265  0.014823509 0.012482387 -0.025907710
266 -0.042892009 0.035377124 -0.018172228
# 残差の共分散行列
resid %>%
    cov(x = ., y = .)
              y1            y2            y3
y1 0.00279961378 0.00032804057 0.00001213196
y2 0.00032804057 0.00041792776 0.00005886082
y3 0.00001213196 0.00005886082 0.00047168243
# 上記共分散行列を手作業で求める。
cov_resid <- data.frame(nrow = 3, ncol = 3)
# 不偏分散
cov_resid[1, 1] <- resid[, 1] %>%
    var()
cov_resid[2, 2] <- resid[, 2] %>%
    var()
cov_resid[3, 3] <- resid[, 3] %>%
    var()
# 不偏共分散
cov_resid[1, 2] <- cov_resid[2, 1] <- sum((resid[, 1] - mean(resid[, 1])) * (resid[, 2] - mean(resid[, 2])))/(nrow(resid) - 1)
cov_resid[1, 3] <- cov_resid[3, 1] <- sum((resid[, 1] - mean(resid[, 1])) * (resid[, 3] - mean(resid[, 3])))/(nrow(resid) - 1)
cov_resid[2, 3] <- cov_resid[3, 2] <- sum((resid[, 2] - mean(resid[, 2])) * (resid[, 3] - mean(resid[, 3])))/(nrow(resid) - 1)
cov_resid
           nrow          ncol            V3
1 0.00279961378 0.00032804057 0.00001213196
2 0.00032804057 0.00041792776 0.00005886082
3 0.00001213196 0.00005886082 0.00047168243

コレスキー分解の対称とする誘導VARモデルの残差の共分散行列

  • 不偏共分散を一旦\(\,n-1\,\)を乗じて戻し、改めて説明変数の数をサンプルサイズから減じた自由度で割った共分散量を\(\,\pmb{\Sigma}_u\,\)とする。
sigma_cov <- summary(out_VAR)$covres
sigma_cov
              y1            y2            y3
y1 0.00294403830 0.00034496330 0.00001275781
y2 0.00034496330 0.00043948752 0.00006189729
y3 0.00001275781 0.00006189729 0.00049601525
# 上記共分散行列を手作業で求める。
# ncol(out_VAR$datamat)で目的変数および説明変数(ドリフト項、トレンド項を含む)の数。
# out_VAR$Kは目的変数の数(内生変数の数)。
# (ncol(out_VAR$datamat) - out_VAR$K)で説明変数の数。
obs <- out_VAR$datamat %>%
    nrow()
cov(resid) * (obs - 1)/(obs - (ncol(out_VAR$datamat) - out_VAR$K))
              y1            y2            y3
y1 0.00294403830 0.00034496330 0.00001275781
y2 0.00034496330 0.00043948752 0.00006189729
y3 0.00001275781 0.00006189729 0.00049601525
sigma_u <- sigma_cov

選択ベクトル

  • ショックはマネタリーベースの撹乱項に発生する設定とする。
select <- c(0, 0, 1)
select
[1] 0 0 1

インパルス応答値の算出

# ショックの大きさを調整するスケールファクター
scale_factor <- 1
# 下三角行列
chol_P <- t(chol(sigma_u))
chol_P
             y1          y2         y3
y1 0.0542589928 0.000000000 0.00000000
y2 0.0063577167 0.019976660 0.00000000
y3 0.0002351281 0.003023649 0.02206394
# 確認
chol_P %*% t(chol_P)
              y1            y2            y3
y1 0.00294403830 0.00034496330 0.00001275781
y2 0.00034496330 0.00043948752 0.00006189729
y3 0.00001275781 0.00006189729 0.00049601525
# 直交化ショック
shock_orth <- chol_P %*% select * scale_factor
shock_orth
         [,1]
y1 0.00000000
y2 0.00000000
y3 0.02206394
# 分析条件設定
num_y <- 3  # 内生変数の数
num_z <- 2  # 外生変数(ドリフト項、トレンド項)の数
num_lag <- 4  # ラグ次数
num_x <- num_lag * num_y + num_z
num_h <- 50  # 観測期数
num_col <- num_h + num_lag
# インパルス応答値(y)と外生変数の初期設定
y <- matrix(0, nrow = num_y, ncol = num_col)
z <- matrix(0, nrow = num_z, ncol = num_col)
h <- num_lag + 1
y[, h] <- shock_orth
for (h in (num_lag + 2):num_col) {
    y[, h] <- B_1 %*% y[, h - 1] + B_2 %*% y[, h - 2] + B_3 %*% y[, h - 3] + B_4 %*% y[, h - 4] + B_z %*% z[, h]
    print(y[, h])
}
[1] -0.0003878982  0.0015055770  0.0260823422
[1] 0.001561643 0.001333325 0.022794297
[1] 0.004278089 0.002072927 0.029191971
[1] 0.005235642 0.003219071 0.032326050
[1] 0.006470273 0.003689741 0.030384313
[1] 0.008314682 0.004129161 0.031528529
[1] 0.009397837 0.004846535 0.033055935
[1] 0.01024196 0.00533843 0.03225201
[1] 0.011338450 0.005705585 0.032021974
[1] 0.012192775 0.006171902 0.032484097
[1] 0.01281486 0.00658345 0.03213768
[1] 0.013482526 0.006903807 0.031707960
[1] 0.014074597 0.007236344 0.031665215
[1] 0.014522301 0.007553405 0.031426115
[1] 0.014938165 0.007817517 0.031047049
[1] 0.015316891 0.008064273 0.030818725
[1] 0.015614226 0.008298521 0.030578405
[1] 0.015865443 0.008501688 0.030259199
[1] 0.016086371 0.008682659 0.029983207
[1] 0.016259771 0.008849132 0.029728779
[1] 0.016393958 0.008994947 0.029444492
[1] 0.016501416 0.009121289 0.029168158
[1] 0.016578585 0.009232973 0.028909197
[1] 0.016626990 0.009329144 0.028643814
[1] 0.016653564 0.009409755 0.028379081
[1] 0.016659460 0.009477275 0.028124253
[1] 0.016645378 0.009532455 0.027871231
[1] 0.016614856 0.009575496 0.027619158
[1] 0.016569905 0.009607693 0.027372676
[1] 0.016511442 0.009630018 0.027129905
[1] 0.016441386 0.009642949 0.026889234
[1] 0.016361438 0.009647293 0.026652316
[1] 0.016272595 0.009643876 0.026419051
[1] 0.016176050 0.009633262 0.026188476
[1] 0.016073029 0.009616056 0.025960957
[1] 0.01596441 0.00959290 0.02573666
[1] 0.015851023 0.009564324 0.025515151
[1] 0.015733708 0.009530816 0.025296391
[1] 0.015613154 0.009492876 0.025080465
[1] 0.015489956 0.009450948 0.024867191
[1] 0.015364688 0.009405434 0.024656456
[1] 0.015237848 0.009356722 0.024448258
[1] 0.01510986 0.00930517 0.02424251
[1] 0.01498112 0.00925110 0.02403911
[1] 0.014851957 0.009194813 0.023838006
[1] 0.014722673 0.009136589 0.023639151
[1] 0.014593523 0.009076681 0.023442462
[1] 0.014464733 0.009015321 0.023247884
[1] 0.014336495 0.008952724 0.023055368
y[, 1:10]
     [,1] [,2] [,3] [,4]       [,5]          [,6]        [,7]        [,8]
[1,]    0    0    0    0 0.00000000 -0.0003878982 0.001561643 0.004278089
[2,]    0    0    0    0 0.00000000  0.0015055770 0.001333325 0.002072927
[3,]    0    0    0    0 0.02206394  0.0260823422 0.022794297 0.029191971
            [,9]       [,10]
[1,] 0.005235642 0.006470273
[2,] 0.003219071 0.003689741
[3,] 0.032326050 0.030384313
y[, 45:ncol(y)]
            [,1]        [,2]        [,3]       [,4]       [,5]        [,6]
[1,] 0.015489956 0.015364688 0.015237848 0.01510986 0.01498112 0.014851957
[2,] 0.009450948 0.009405434 0.009356722 0.00930517 0.00925110 0.009194813
[3,] 0.024867191 0.024656456 0.024448258 0.02424251 0.02403911 0.023838006
            [,7]        [,8]        [,9]       [,10]
[1,] 0.014722673 0.014593523 0.014464733 0.014336495
[2,] 0.009136589 0.009076681 0.009015321 0.008952724
[3,] 0.023639151 0.023442462 0.023247884 0.023055368
out_y <- y[, (num_lag - 1):num_col]
irf_orth <- t(out_y)
y_min <- min(irf_orth)
y_max <- max(irf_orth)
x_data <- matrix(-1:num_h, nrow = (num_h + 2), ncol = 1)
matplot(x_data, irf_orth, type = "l", lwd = 2, col = 1, lty = c("solid", "dashed", "dotted"), xlim = c(-1, num_h), ylim = c(y_min, y_max), xlab = "Time Horizon", ylab = "Impulse Response", main = "Orthogonal Impulse Responses: impulse = y3:マネタリーベース")
abline(h = 0, col = "gray")
Figure 1

実線:y1 日経平均株価、破線:y2 ドル円為替レート、点線:y3 マネタリーベース

関数irf {vars}によるインパルス応答

irf(x = out_VAR, impulse = "y3", n.ahead = 50, ortho = T, boot = F) %>%
    plot()
Figure 2

参照引用資料

  1. 村尾博(2019),『Rで学ぶVAR実証分析』,オーム社,pp.249-284
  2. https://dl.ndl.go.jp/view/download/digidepo_11172758_po_r_59_074_140.pdf?contentNo=1&alternativeNo=
  3. https://doshisha.repo.nii.ac.jp/?action=repository_action_common_download&item_id=26491&item_no=1&attribute_id=28&file_no=1

最終更新

Sys.time()
[1] "2024-04-16 05:06:40 JST"

R、Quarto、Package

R.Version()$version.string
[1] "R version 4.3.3 (2024-02-29 ucrt)"
quarto::quarto_version()
[1] '1.4.542'
packageVersion(pkg = "tidyverse")
[1] '2.0.0'

著者